Incorporating first-principles quantum chemistry data in kinetic Monte Carlo simulations has proven to be a powerful approach in investigating the behaviour of catalytic systems at the molecular level. Such first-principles KMC frameworks were pioneered by M. Neurock, M. Scheffler and co-workers [M. Neurock, E. W. Hansen (1998), Comp. Chem. Eng. 22: S1045-S1060; K. Reuter, D. Frenkel, M. Scheffler (2004), Phys. Rev. Lett. 93(11): 116105], and make use of the energies computed typically from density functional theory (DFT) for stable molecular species and transition states, in order to calculate rate constants. This tutorial explains how to map quantum chemistry data into energetics input in Zacros. As a working example we will consider water-gas shift pathways on Pt(111).
An energetics model in KMC simulation consists of the energies of gas species, transition states, as well as stable surface species and the lateral interactions between them. Information about the energetics is typically obtained via density functional theory (DFT) calculations within the first-principles KMC framework. In the following, we will focus on the energetics of gas species, surface species at the zero-coverage limit (no spectators in close proximity), and the transition states (for calculating activation energies). Lateral interactions will be discussed to some extent as well. We will explain how one can map data obtained from DFT calculations on the water-gas shift on Pt(111) into Zacros input for files simulation_input.dat, energetics_input.dat and mechanism_input.dat. If you are unfamiliar with the structure of these files, please refer to the tutorial Ziff-Gulari-Barshad Model in Zacros.
Part 1: Modelling assumptions and DFT data
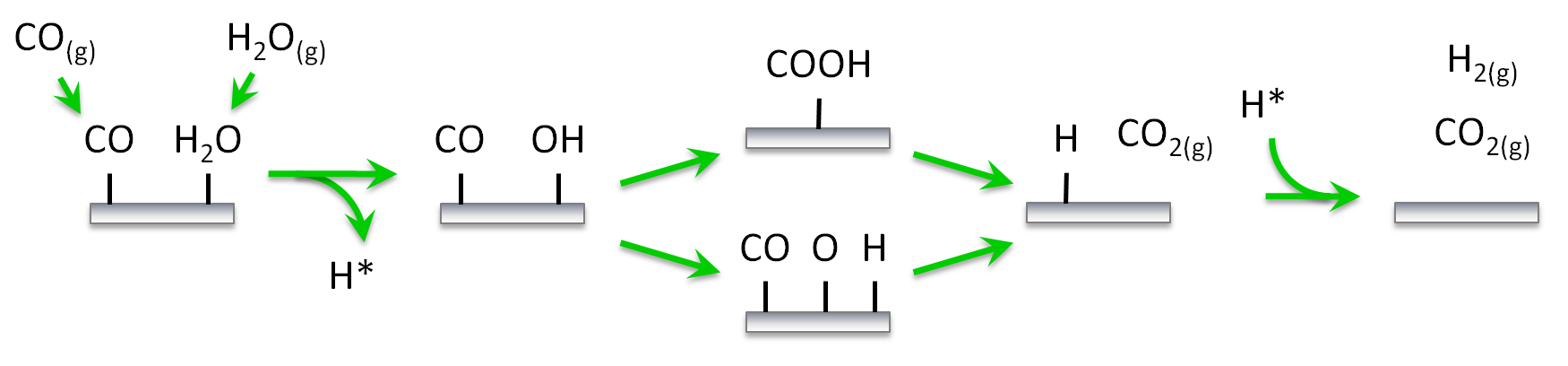
The first pathway we would like to investigate (shown schematically below) involves carboxyl (COOH) as the key intermediate for the water gas shift reaction on Pt(111). The key steps are the adsorption of CO and H2O on the surface, the decomposition of H2O into OH and H, the reaction between CO and OH to form COOH, the decomposition of the latter towards CO2 and H, and the associative desorption of H2. The second pathway includes the dissociation of OH further into O and H and the CO oxidation by O. The data are based on our previous work on water-gas shift,1 although we have made some simplifications for the purposes of this tutorial. Thus, we will assume that: (i) the catalytic surface can be represented by a lattice of equivalent sites (single site type), (ii) dissociative adsorption events are not activated, (iii) lateral interactions are limited to 1st nearest neighbour range and involve only a few key species participating in these pathways, (iv) the unit cell is large enough so that interactions of adsorbates with their periodic images can be ignored. With regard to assumption (i), accounting for more than one site types on catalytic models is straightforward, it may however, require extra care and diligent book-keeping. Assumption (ii) is also made for simplicity in this tutorial, but it is easy to consider transition states for dissociative adsorption events. Assumptions (iii) and (iv) are also oversimplifications for the purposes of this tutorial. Fitting cluster expansions with longer-range interactions, and by taking into account the periodic images will be covered in another tutorial. Moreover, we will not concern ourselves with zero-point energy (ZPE) corrections, these can be added in a straightforward way and everything we discuss applies to the ZPE-corrected energies as well.
The tables below show the energies computed for the species of interest by software package SIESTA (for computational details see Ref. 1).
| Catalytic Surface | DFT Energy (eV) |
|---|---|
| Pt(111) | -11448.220 |
| Gas Species | DFT Energy (eV) |
|---|---|
| CO | -588.789 |
| H2O | -467.460 |
| H2 | -31.403 |
| CO2 | -1025.462 |
| O2 | -867.202 |
| Surface Species | DFT Energy (eV) |
|---|---|
| CO* | -12039.087 |
| H2O* | -11916.042 |
| OH* | -11899.149 |
| O* | -11882.980 |
| H* | -11464.540 |
| COOH* | -12490.256 |
| Co-Adsorbed Species (1NN) | DFT Energy (eV) |
|---|---|
| CO*+CO* | -12629.394 |
| OH*+H* | -11915.448 |
| O*+H* | -11899.102 |
| CO*+OH* | -12489.950 |
| CO*+O* | -12473.424 |
| Transition States | DFT Energy (eV) |
|---|---|
| TS1: H2O*→OH*+H* | -11915.265 |
| TS2: OH*→O*+H* | -11898.209 |
| TS3: CO*+OH*→COOH* | -12489.544 |
| TS4: COOH*→CO2+H* | -12489.404 |
| TS5: CO*+O*→CO2 | -12472.435 |
In the following section we will discuss how to choose a set of reference species with respect to which the formation energies of all species will be calculated.
Part 2: Choosing a reference
The first thing we need to do is decide on a reference set of species; all the DFT-computed energies will then be mapped into formation energies, which are essentially energy differences with respect to these reference species. To decide how many reference species we need and which these species should be the following rules are useful:
- The pristine catalytic phase (facet, nano-cluster etc. with nothing adsorbed) has to be included in the reference set.
- The rest of the reference species will be gas phase species, and we need as many such species as the number of different atoms encountered in our species.
- The reference species must have linearly independent compositions. This means that we should not be able to write a reaction that produces one (or more) reference species from other reference species.
In our case, we have a Pt surface as the catalyst and C-, H-, and O-containing species. According to rule 1, Pt(111) will be in our reference set. In terms of the gas species of rule 2, perhaps the easiest choice of a reference set is the one used in thermodynamics: in our case, that would be atomic C and the diatomics O2 and H2. Such a basis might not be very convenient, however, in practical terms. For instance, the triplet state of O2 is not accurately captured by DFT, so this might not be a good reference species. Also, it is frequently convenient to have the reactant gas molecules in the basis so that the corresponding bound species’ formation energies are equal in magnitude to the binding energies with opposite sign. So in our case, we will choose as our reference the gas species CO, H2O and H2. It can be verified that rule 3 holds true. An alternative option would be CO, H2O and CO2. An invalid option would be CO, CO2 and O2: these molecules’ compositions are not linearly independent (we can write the CO oxidation reaction), and also H-containing molecules remain unreferenced.
In the following, we will work with the reference set {Pt(111), CO, H2O, H2}.
To better understand the purpose of the “reference set”, an analogy with the idea of a “basis set” would perhaps be useful: one can think of the set of reference species as a basis (in terms of stoichiometric compositions), out of which we can “construct” any other species we are interested in. The construction process would involve first determining which and how many basis/reference molecules we need and then simply rearranging atoms in order to form the species of interest. These ideas can be formalised mathematically using vectors to represent the composition of a species in terms of its constituent elements. Given a basis on the space of species’ compositions, any other species can be represented as a linear combination of the basis vectors.
Part 3: Calculating formation energies
The formation energy of a molecular species/configuration is the energy required for (or released while) generating that configuration from molecules within the reference set. We must note that what we refer to as “formation energy”, is different than the (Gibbs) free energy of formation, or the heat (enthalpy) of formation, used in Physical Chemistry. The free energy and the enthalpy include contributions from translational, rotational, and vibrational degrees of freedom. In our case, we work exclusively with energies provided by a DFT code, which are potential energies within the framework of the Born-Oppenheimer approximation. Roughly speaking, the latter allows us to fix the positions of the nuclei and calculate the energy of the system as the sum of the kinetic energy of the electronic cloud and the energies from the Coulomb interactions between electrons and nuclei.
Going back to the calculation of the formation energies, by the definition of the previous paragraph, it is clear that the formation energy of any reference species is zero. On the other hand, the energy of an adsorbed species, for instance CO* would be:
FE[CO*] = E[CO*] – { E[Pt(111)] + E[CO] }
In the above equation, FE[A] stands for formation energy of species A, E[A] means the DFT-computed energy of A. Thus to compute the formation energy of CO*, we take the DFT energy of CO* and subtract the DFT energies of pristine Pt(111) and CO gas. This was an easy example, since CO gas is a reference species. What about the energy of COOH*, as species which is not within the reference set? Its formation energy is defined as:
FE[COOH*] = E[COOH*] – { E[Pt(111)] + E[CO] + E[H2O] – ½ E[H2] }
Notice that we calculated the COOH* species formation energy with respect to a linear combination of reference species energies. This linear combination is determined by the composition stoichiometry: one CO plus one H2O minus half an H2 gives us precisely the same number of C, O, H atoms as in the COOH molecule. For a proper reference set, this linear combination is unique, making the definition of formation energies unambiguous.
In the table below we present the formation energies of all species calculated in a similar way as outlined above. Highlighted in light red are the DFT energies of reference species.
| Catalytic Surface | DFT Energy (eV) | Form. Energy (eV) |
|---|---|---|
| Pt(111) | -11448.220 | 0.000 |
| Gas Species | DFT Energy (eV) | Form. Energy (eV) |
|---|---|---|
| CO | -588.789 | 0.000 |
| H2O | -467.460 | 0.000 |
| H2 | -31.403 | 0.000 |
| CO2 | -1025.462 | -0.615 |
| O2 | -867.202 | 4.913 |
| Surface Species | DFT Energy (eV) | Form. Energy (eV) |
|---|---|---|
| CO* | -12039.087 | -2.077 |
| H2O* | -11916.042 | -0.362 |
| OH* | -11899.149 | 0.830 |
| O* | -11882.980 | 1.298 |
| H* | -11464.540 | -0.619 |
| COOH* | -12490.256 | -1.487 |
| Co-Adsorbed Species (1NN) | DFT Energy (eV) | Form. Energy (eV) |
|---|---|---|
| CO*+CO* | -12629.394 | -3.595 |
| OH*+H* | -11915.448 | 0.233 |
| O*+H* | -11899.102 | 0.877 |
| CO*+OH* | -12489.950 | -1.181 |
| CO*+O* | -12473.424 | -0.357 |
| Transition States | DFT Energy (eV) | Form. Energy (eV) |
|---|---|---|
| TS1: H2O*→OH*+H* | -11915.265 | 0.416 |
| TS2: OH*→O*+H* | -11898.209 | 1.770 |
| TS3: CO*+OH*→COOH* | -12489.544 | -0.776 |
| TS4: COOH*→CO2+H* | -12489.404 | -0.635 |
| TS5: CO*+O*→CO2 | -12472.435 | 0.632 |
Part 4: Pairwise interaction energies
Let us now focus our attention on one of the co-adsorbed configurations, in particular CO*-CO*. This configuration contains two CO adsorbates as 1st nearest-neighbours. The formation energy of this configuration was calculated as:
FE[CO*+CO*] = E[CO*+CO*] – { E[Pt(111)] + 2 E[CO] }
If these CO* molecules were placed on the surface far away from each other, the formation energy would be equal to twice the formation energy of CO*, namely -4.155 eV. However, because of the pairwise repulsive interaction that these molecules “feel” when in close proximity, the energy of the co-adsorbed configuration is higher (-3.595 eV). The difference of 0.560 is called the “interaction energy” between the CO*-CO* pair. Note that we have assumed that the DFT calculation cell is large, so that the only adsorbate-adsorbate lateral interaction is between these two CO* molecules (no interactions with periodic images). The magnitude of this pairwise interaction energy is therefore:
IE[CO*+CO*] = FE[CO*+CO*] – 2 FE[CO*]
where IE[A+B] stands for the interaction energy between A and B. It can easily be verified that:
IE[CO*+CO*] = E[CO*+CO*] – 2 E[CO*] + E[Pt(111)]
Similarly, the interaction between different species, for instance CO*+OH* is calculated as:
IE[CO*+OH*] = FE[CO*+OH*] – { FE[CO*] + FE[OH*] }
Note that 1st nearest-neighbour pairwise additive interactions are not enough to accurately capture the energetics of the adsorbate layer: longer-range pairwise interactions as well as many-body contributions may be significant (see tutorial Cluster Expansion for Oxygen on Pt(111)). Pairwise interactions are a good start, however, and it is useful to be able to compute a first estimate thereof with the approach just discussed. In the following table, we present the interaction energies for our co-adsorbed configurations:
| Co-Adsorbed Species (1NN) | DFT Energy (eV) | Form. Energy (eV) | Inter. Energy (eV) |
|---|---|---|---|
| CO*+CO* | -12629.394 | -3.595 | 0.560 |
| OH*+H* | -11915.448 | 0.233 | 0.021 |
| O*+H* | -11899.102 | 0.877 | 0.198 |
| CO*+OH* | -12489.950 | -1.181 | 0.066 |
| CO*+O* | -12473.424 | -0.357 | 0.423 |
Part 5: Activation energies
Next, let us discuss how the formation energies of transition states are mapped into activation energies. Let us focus on the H2O dissociation reaction. The formation energy of the corresponding transition state (TS1) was calculated to be 0.416 eV. The initial state of this reaction is adsorbed H2O, with a formation energy of -0.362 eV. The activation energy for this reaction is simply the formation energy of the transition state minus the energy of the initial state:
Ea,fwd,1 = AE[H2O*→OH*+H*] = FE[TS1] – FE[H2O*]
This gives a value of 0.777 eV. It can be easily verified that:
Ea,fwd,1 = E[TS1] – E[H2O*]
Note that we only care about the forward activation energy. If the event is reversible, Zacros will be able to calculate the reverse activation energy, Ea,rev,1, as the forward one minus the delta-energy of the reaction, ΔE1. The latter can be easily calculated since the formation energies of initial and final state species are known (as well as the pertinent interaction energies if applicable).
The case just noted was easy, as we only had one reactant molecule in the initial state. Let us examine a case with two molecules, namely CO*+OH* reacting towards COOH*. The activation energy is calculated as:
Ea,fwd,3 = AE[CO*+OH*→COOH*] = FE[TS3] – FE[CO*+OH*]
The resulting value is 0.405 eV. Notice that from the formation energy of TS3 we subtract the formation energy of the co-adsorbed CO*+OH* configuration, which includes the pairwise interaction energy between CO* and OH*, rather than the sum of the formation energies of CO* and OH*. This is physically meaningful as CO* and OH* have to be in close proximity in order to react. This is how Zacros understands the activation energy as well; if the COOH* formation reaction happens on an empty surface, Zacros will use the value of 0.405 eV (activation energy at the zero-coverage limit), and will not add the interaction energy between the reactive of CO*-OH* on top of that value. However, if spectator species (not participating in the reaction) exist in the neighbourhood and exert attractive or repulsive interactions, then the activation energy will be different than 0.405 eV (this is modelled by Brønsted-Evans-Polanyi relations, which are out of the scope of this tutorial).
In the following table we present the activation energies of the four reactions of interest:
| Transition States | DFT Energy (eV) | Form. Energy (eV) | Activ. Energy (eV) |
|---|---|---|---|
| TS1: H2O*→OH*+H* | -11915.265 | 0.416 | 0.777 |
| TS2: OH*→O*+H* | -11898.209 | 1.770 | 0.940 |
| TS3: CO*+OH*→COOH* | -12489.544 | -0.776 | 0.405 |
| TS4: COOH*→CO2+H* | -12489.404 | -0.635 | 0.852 |
| TS5: CO*+O*→CO2 | -12472.435 | 0.632 | 0.988 |
Part 6: Zacros input
Let us take a moment to summarise what we have done so far. We started from a dataset containing the DFT-computed energies for gas and surface species participating in the water-gas shift reaction on Pt(111). The dataset also contained the energy of the clean Pt(111) surface (Part 1). We subsequently chose a reference set of species, according to the rules of Part 2, and calculated the formation energies of all our species with respect to the reference (Part 3). Using these formation energies, we were further able to compute pairwise interaction energies between co-adsorbed species, and activation energies for elementary reactions.
We will shortly discuss how these numbers are translated into Zacros input. For convenience, we have compiled all our data and calculated values into the table below. The numbers highlighted with orange will be used in the Zacros input files.
| Catalytic Surface | DFT Energy (eV) | Form. Energy (eV) |
|---|---|---|
| Pt(111) | -11448.220 | 0.000 |
| Gas Species | DFT Energy (eV) | Form. Energy (eV) |
|---|---|---|
| CO | -588.789 | 0.000 |
| H2O | -467.460 | 0.000 |
| H2 | -31.403 | 0.000 |
| CO2 | -1025.462 | -0.615 |
| O2 | -867.202 | 4.913 |
| Surface Species | DFT Energy (eV) | Form. Energy (eV) |
|---|---|---|
| CO* | -12039.087 | -2.077 |
| H2O* | -11916.042 | -0.362 |
| OH* | -11899.149 | 0.830 |
| O* | -11882.980 | 1.298 |
| H* | -11464.540 | -0.619 |
| COOH* | -12490.256 | -1.487 |
| Co-Adsorbed Species (1NN) | DFT Energy (eV) | Form. Energy (eV) | Inter. Energy (eV) |
|---|---|---|---|
| CO*+CO* | -12629.394 | -3.595 | 0.560 |
| OH*+H* | -11915.448 | 0.233 | 0.021 |
| O*+H* | -11899.102 | 0.877 | 0.198 |
| CO*+OH* | -12489.950 | -1.181 | 0.066 |
| CO*+O* | -12473.424 | -0.357 | 0.423 |
| Transition States | DFT Energy (eV) | Form. Energy (eV) | Activ. Energy (eV) |
|---|---|---|---|
| TS1: H2O*→OH*+H* | -11915.265 | 0.416 | 0.777 |
| TS2: OH*→O*+H* | -11898.209 | 1.770 | 0.940 |
| TS3: CO*+OH*→COOH* | -12489.544 | -0.776 | 0.405 |
| TS4: COOH*→CO2+H* | -12489.404 | -0.635 | 0.852 |
| TS5: CO*+O*→CO2 | -12472.435 | 0.632 | 0.988 |
Gas species: formation energies
The formation energies of the gas species are defined in file simulation_input.dat using the keyword gas_energies. The block of instructions for defining the gas species of our example would be (for more details on each of the keywords please refer to the tutorial Ziff-Gulari-Barshad Model in Zacros):
n_gas_species 5
gas_specs_names CO H2O H2 CO2 O2
gas_energies 0.000 0.000 0.000 -0.615 4.913 # in eV
gas_molec_weights 28.0102 18.0153 2.0159 44.0096 31.9988
gas_molar_fracs 1.00e-5 0.950 0.000 0.000 0.000
Surface species: formation energies and lateral interactions
The formation energies of the surface-bound species along with any pertinent lateral interactions are defined in file energetics_input.dat. Zacros uses a cluster-Hamiltonian type of approach for capturing lattice energetics (more about this on the tutorial Cluster Expansion for Oxygen on Pt(111)). This approach decomposes the total energy of the lattice into single-, two-, and many-body contributions, referred to as “figures” or “clusters”. Each such cluster is defined using blocks of instructions between keywords cluster...end_cluster. For instance, the instructions for defining the cluster representing bound H2O in our example would be:
cluster H2O_Point
sites 1
lattice_state
1 H2O* 1
cluster_eng -0.362
end_cluster
Similarly, the instructions for defining a cluster representing the repulsive interaction between bound CO and OH would be:
cluster CO-OH_1NN
sites 2
neighboring 1-2
lattice_state
1 CO* 1
2 OH* 1
cluster_eng 0.066
end_cluster
In the example above the cluster contained molecules of different species. If we wanted to define the interaction between a pair of molecules (both of the same species) we would use the same construct with the additional setting of the graph multiplicity:
cluster CO_pair_1NN
sites 2
neighboring 1-2
lattice_state
1 CO* 1
2 CO* 1
graph_multiplicity 2
cluster_eng 0.560
end_cluster
The graph multiplicity of 2 specifies that whenever Zacros detects an instance of this pattern, it will add a contribution equal to 0.560/2 eV in the total energy of the lattice. Since the pattern is symmetric, it will be detected twice, resulting in the correct contribution of 0.560 eV per distinct CO*-CO* pair. If we did not specify the graph multiplicity, Zacros would have used the default value of 1, adding 0.560 eV twice to the total energy of the lattice. More information is provided in “Part 3: Input for two-body terms” of the tutorial Cluster Expansion for Oxygen on Pt(111).
Reactions: activation energies
Finally, let us discuss how the activation energies are used in the Zacros input. These parameters, along with the mechanistic information about the elementary steps are contained in file mechanism_input.dat. Each elementary steps is defined by a block of instructions enclosed within keywords step...end_step, for irreversible steps, or reversible_step...end_reversible_step, for reversible steps. It is advisable to always use reversible steps in specifying a mechanism, so that the simulation satisfies microscopic reversibility and thermodynamic consistency. In our example, if we wanted to define for instance H2O dissociation, we would write:
reversible_step H2O_dissociation
sites 2
neighboring 1-2
initial
1 H2O* 1
2 * 1
final
1 OH* 1
2 H* 1
pre_expon 1.042e+13
pe_ratio 1.000e+00
activ_eng 0.777
end_reversible_step
We will only make a few brief comments here; for more details please refer to “Part 4: Reaction mechanism” of the tutorial Ziff-Gulari-Barshad Model in Zacros. Notice that we defined this as a two-site event, since there will have to be a neighbouring empty site available for the dissociation of the H2 molecule. To calculate the rate constant of the forward step of any reversible reaction, Zacros uses the Arrhenius equation:
where kfwd is the rate constant, Afwd is the pre-exponential, Ea,fwd the activation energy, kB is Boltzmann's constant, and T is the temperature. A similar equation applies to the reverse step. As shown in the above block of instructions, Zacros allows to define the forward pre-exponential (pre_expon), the ratio between forward and reverse pre-exponentials (pe_ratio). and the forward activation energy (activ_eng). In our case we have calculated an estimated value of the pre-exponentials (same value for forward and reverse), by evaluating the expression kBT/hPlanck at 500 K (see the supplementary materials of Refs. 2 and 3 for more information about calculating pre-exponentials). We further use the activation energy value as computed above.
As another example, let us define the COOH* decomposition into gas CO2 and H* as an irreversible step. As noted before, it is preferable to define all steps as reversible; yet our choice to treat this decomposition step as irreversible will not create any problems if we only care about the forward water-gas shift reaction with no CO2 in the gas phase. The instructions defining this step are:
step COOH_decomposition
gas_reacs_prods CO2 1
sites 1
initial
1 COOH* 1
final
1 * 1
pre_expon 1.042e+13
activ_eng 0.852
end_step
Notice that for this step we did not have to define a pre-exponential ratio. On the other hand, we had to define explicitly the gas product of this reaction (CO2) using the keyword gas_reacs_prods.
Finally, let us look into an adsorption/desorption step, for instance for H2O:
reversible_step H2O_adsorption
gas_reacs_prods H2O -1
sites 1
initial
1 * 1
final
1 H2O* 1
pre_expon 2.776e+07
pe_ratio 2.665e-06
activ_eng 0.000
end_reversible_step
The adsorption step is spontaneous, so we specified an activation energy of zero. The pre-exponential was calculated by the following equation:
where Asite is the effective area of the catalytic site (taken here as 1 Ų), and m is the mass of the adsorbing molecule (also T = 500 K, as before). This expression for the pre-exponential has units of inverse pressure inverse time (bar-1s-1). Zacros multiplies this value with the partial pressure of the adsorbing gas species in order to calculate the rate constant of the adsorption event.
Desorption is represented in Zacros as the reverse step of the event defined above. Thus, when Zacros encounters a bound H2O molecule on the lattice, it will add such a desorption in the queue of possible lattice processes. The activation energy of this step at the zero-coverage limit will be equal to the formation energy of H2O gas minus that of H2O* (the binding energy of water, 0.362 eV). In this particular example, the activation energy of water dissociation will be the same even in the presence of spectator adsorbates, since we have not defined any interactions of H2O* with other species.
Download the four Zacros input files of this example.
References
- M. Stamatakis, Y. Chen and D. G. Vlachos (2011). “First Principles-Based Kinetic Monte Carlo Simulation of the Structure-Sensitivity of the Water-Gas Shift Reaction on Platinum Surfaces”. Journal of Physical Chemistry C 115(50): 24750-24762 (doi: 10.1021/jp2071869)
- M. Stamatakis and D. G. Vlachos (2011). “A Graph-Theoretical Kinetic Monte Carlo Framework for on-Lattice Chemical Kinetics”. Journal of Chemical Physics 134(21): 214115 (doi: 10.1063/1.3596751); Supplementary Material
- M. Stamatakis and D. G. Vlachos (2012). “Unraveling the Complexity of Catalytic Reactions via Kinetic Monte Carlo Simulation: Current Status and Frontiers”. ACS Catalysis 2(12): 2648-2663 (doi: 10.1021/cs3005709); Supplementary Material