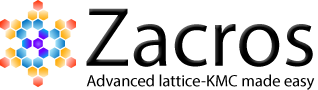What's KMC All About and Why Bother

Beyond simple: the real power of KMC

The previous section demonstrates what kind of output can KMC generate, and shows that for very simple systems, which can be modelled analytically, the KMC predictions are in perfect agreement with the analytical results (e.g. from Langmuir-Hinshelwood modelling). So what is the motivation for using KMC in the first place? The answer is simple: catalytic systems are complex! Much more complex than what the Langmuir-Hinshelwood model suggests. Even well-studied (and deceptively simple) reactions, like the CO oxidation, exhibit rich and often puzzling behaviour as recent experimental research has demonstrated. KMC modelling has helped unravel such behaviour and explain the experimental observations. In the following, we summarize modelling contributions from our team on the CO oxidation reaction on two classes of materials (Pd surface, Au nanoclusters), highlighting the advantages of KMC against simple models. The discussion is kept at a high-level, intended to "whet the appetite" of the newly initiated reader, who can consult the cited papers for more technical details.

CO oxidation on Pt(111): a deceptively simple system

A major assumption in Langmuir-Hinshelwood type of models is that the adlayer is ideal and well-mixed. However, the presence of adsorbate-adsorbate lateral interactions leads to spatial correlations and coverage-dependent activation energies. KMC simulation was recently employed to show that such effects can shape the observed kinetics, most notably, the reaction order.^2,3 The study was motivated by an experiment carried out by Nakai, Kondoh and co-workers, who dosed the Pt(111) surface with oxygen, exposed the system to a CO atmosphere and measured several kinetic parameters (orders with respect to CO_(g) and O*, apparent activation energies) while also observing the structure of the adlayer through XPS.⁴ What was particularly interesting, was the different reaction orders with respect to O* at high and low temperatures (320 K, 190 K). At the high temperature, the experiment showed half-order kinetics which were attributed to the formation of O* islands that react with CO* only at their periphery. The length of the periphery scales with the square root of their area, and the total area is proportional to the O* coverage; therefore, this simple geometric argument should be enough to explain the observed half-order kinetics with respect to O* coverage at 320 K. However, observations at 190 K showed first-order reaction kinetics with respect to O*, which indicated a well-mixed adlayer. This is where things become counter-intuitive: why would one expect to see islands at 320 K, but not at 190 K? If anything, one would expect the islands to be even more stable at the low temperature, in which case, one would measure half-order kinetics at 190 K as well.

The problem with these arguments is that they completely neglect the effect of lateral interactions on the activation barriers and reaction rates. Detailed first-principles-based⁵ KMC modelling suggests that in both the high and low temperatures, the adlayer remains relatively well-mixed: as the CO molecules impinge at random positions on the surface, any oxygen clusters quickly dissipate. This "almost well-mixed" behaviour has a positive contribution to the reaction order of 0.9 at 320 K and 0.8 at 190 K (recall that an order of 1.0 means "totally well-mixed" adlayer, and 0.5 means "completely segregated"). However, the effect of lateral interactions on the activation energies is decisive. At the high temperature, the system exhibits mean-field type behaviour; since CO-CO interactions are slightly more strongly repulsive than the other adsorbate-adsorbate interactions, the reactive CO becomes more and more destabilized as the reaction proceeds, making the reaction "go faster" as oxygen gets depleted from the surface (top left panel of figure below). This manifests as a negative contribution to the overall reaction order of about -0.4, bringing the total order to 0.5, half order kinetics! On the other hand, at the low temperature, one has to look into the entire distribution of activation energies as time goes by (bottom right panel of figure below). Proper averaging of the elementary event rates in the presence of these lateral interactions shows that the effect of oxygen coverage is positive (the reaction slows down as oxygen gets depleted; top right panel of figure below), with a total reaction order of about unity.

Looking at the histograms of the bottom two panels above, it is worth noting that in the presence of these coverage effects, the activation energy follows a distribution, rather than being equal to a single value. The average is shown by the red vertical lines, and it is evident that there are events with much higher activation energies, but also events with much lower activation energies. The latter contribute much more to the observed overall rate.

CO oxidation on Au nanoclusters

In the previous system, the catalyst was an extended flat surface and complications arose from the presence of lateral interactions. Things become even more complicated when we look at nanoscale or subnanoscale catalysts. Au (gold) nanoclusters are an excellent example to consider: such clusters expose a variety of sites which have different coordination numbers and therefore different chemical behaviours. The underlying pathways of the CO oxidation chemistry can be rather intricate, involving changes in the morphology of the material (catalyst reconstruction), species that bind to more than one site, competitive routes towards the same product (CO₂) but also undesired poisons (such as carbonate, CO₃). In addition, talking about coverage in subnanoscale Au clusters becomes tricky: because of the small number of sites, coverage is no longer a continuous variable; it may actually exhibit a "rather discrete" behaviour, e.g. on Au₆ the coverage of CO (which binds to top sites; see lattices below) can take only 7 values, 0, 1/6, 2/6,...,1. Therefore, constructing a simple kinetic model formulated as an ordinary differential equation (ODE) becomes problematic: while one could consider the average coverage on an ensemble of such Au₆ clusters, but still they would have to start from a detailed discrete model and try some sort of averaging procedure to get to the ODE model.

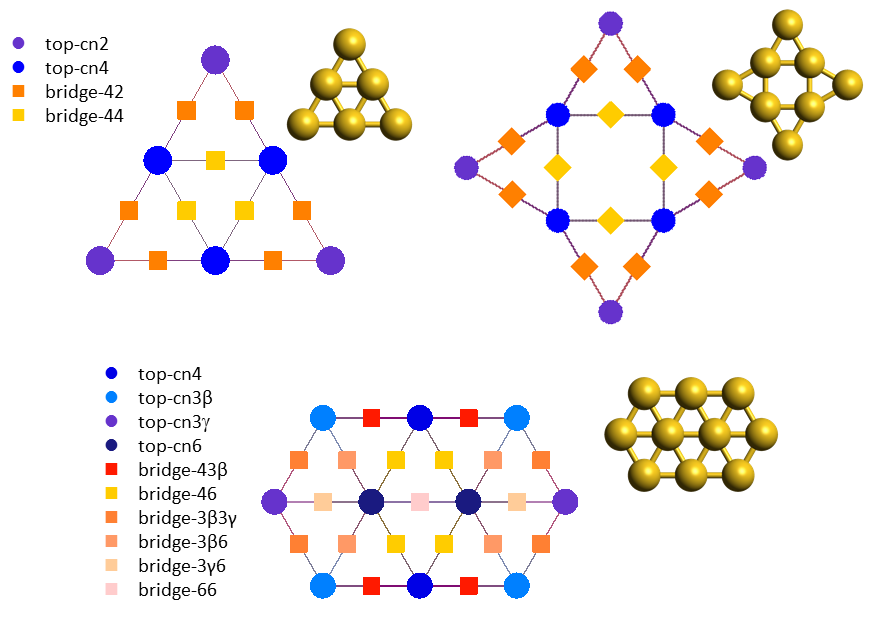
Kinetic Monte Carlo is essentially this "detailed discrete model". Using first-principles KMC models of three Au structures, Au₆, Au₈ and Au₁₀ (the molecular structures and KMC lattices of which are depicted above), it was possible to perform an in-depth investigation of the kinetics leading to the puzzling reactivity trends observed in experiments. In particular, even though all these clusters expose undercoordinated sites, Au₆ appears as inactive, whereas Au₈ and Au₁₀ show high activities, with Au₈ more catalytically active than Au₁₀ towards CO oxidation.^6,7 DFT calculations and KMC simulations exposing the Au clusters to a reactants mixture that contains only CO and O₂, showed that Au₆ gets poisoned by carbonate early on, whereas Au₈ and Au₁₀ do not. On Au₈ two parallel oxidation pathways were found to contribute to the activity, with one of the pathways involving catalyst reconstruction. On Au₁₀, a sequence of two elementary steps were found to be rate limiting and lead to the lower activity of this structure compared to Au₈. These two steps were: the tilting of O₂ from the more stable bidentate to a less stable monodentate configuration, and the subsequent reaction thereof with CO towards CO₂.