Cluster Expansion for Oxygen on Pt(111)

Part 3: Input for two-body terms

Nearest-neighbour interactions and the concept of graph multiplicity

Let us now proceed with the two-body terms. Following the rules of the previous section, we can draw the schematic of the 1NN interaction pattern, shown previously in Part 1:

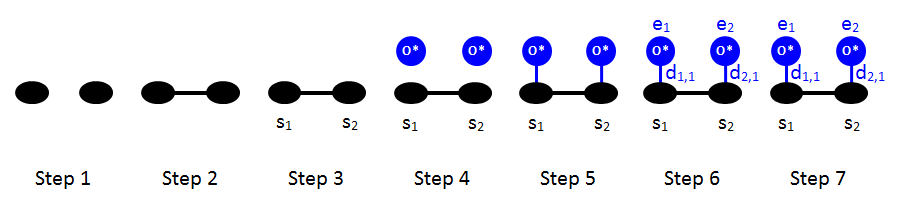
The Zacros input for this cluster is shown below.

cluster O_pair_1NN
  sites 2
  neighboring 1-2
  lattice_state
    1 O*   1
    2 O*   1
  site_types          fcc_t  fcc_t
  graph_multiplicity  2
  cluster_eng         0.140
end_cluster

The new keyword neighboring specifies that sites 1 and 2 must be neighbours in the pattern. Moreover, since there are two sites in the pattern, there are now two lines following lattice_state. The first line corresponds to site 1 and the second to site 2. In each line, the first word is the entity number, the second is the species type, and the third is the dentate occupying the corresponding site. In line with the above figure, our input specifies that site 1 is occupied by entity 1, which is an oxygen adatom, and binds therein with dentate 1 (the only dentate for this species). Moreover, site 2 is occupied by entity 2, which is an oxygen adatom, and binds therein with dentate 1.

Some discussion on the graph multiplicity is useful at this point. When Zacros computes the total energy of the system, it has to detect all the occurrences of the known (i.e. defined in the input) energetic interaction patterns on the lattice. To do so, it solves a sequence of subgraph isomorphism problems, trying to match the known pattern with arrangements of adsorbates on the lattice. If a given pattern is symmetric, the subgraph isomorphism problem may give the same solution more than once. Consider for example the following arrangement of a pair of oxygen adatoms on a lattice with 30 sites:

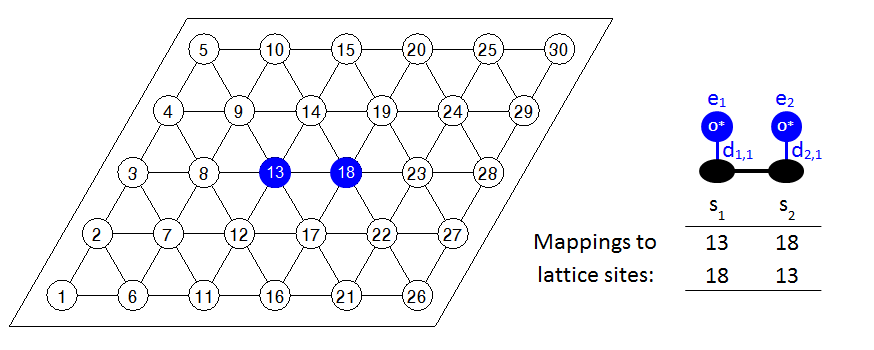
Zacros will detect that this is a 1NN pair of sites and will assign lattice-site 13 as pattern-site 1 and lattice-site 18 as pattern-site 2. However, there is no reason why lattice-site 18 can't be pattern-site 1, and lattice-site 13 pattern-site 2. In fact, this combination will be detected as another valid pattern by Zacros. We therefore see that the same pattern is detected twice, because of the symmetric arrangements of adsorbates therein. Consequently, the graph multiplicity is defined as the number of times a distinct pattern is detected by solving the subgraph isomorphism problem. In our case, the graph multiplicity is 2, so Zacros will add a contribution of 0.070 eV (0.140/2) per pattern to the energy of the system, bringing the total contribution to the correct value of 0.140 eV.

Long-range interactions: variants, angles and sites with unspecified state

We move on to the specification of long-range pairwise additive interactions, which are slightly more complicated. Consider the 2NN and 3NN patterns displayed below:

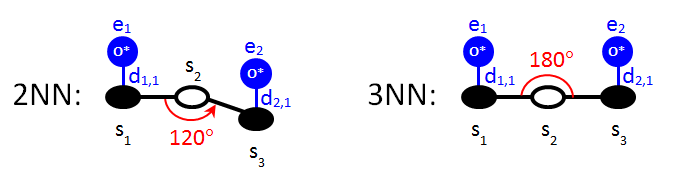
Both patterns involve three sites; the first and the third are occupied by oxygen and the second site has an unspecified state. Site 1 neighbours with site 2, and site 2 neighbours with site 3. The only difference between these two patterns is the angle between the vectors s₂→s₁ and s₂→s₃. Of course, the ECIs of the patterns are different as well. To make the input more concise, one can use the keyword variant. The Zacros input for these two patterns can be thus combined into one block that reads as follows:

cluster O_pair
  sites 3
  neighboring 1-2 2-3
  lattice_state
    1 O*   1
    & &    &
    2 O*   1

  variant 2NN
    site_types          fcc_t  fcc_t  fcc_t
    graph_multiplicity  2
    angles              1-2-3:120.0
    cluster_eng         0.032
  end_variant

  variant 3NN
    site_types          fcc_t  fcc_t  fcc_t
    graph_multiplicity  2
    angles              1-2-3:180.0
    cluster_eng        -0.016
  end_variant

end_cluster

In the first part of this block, we specify the number of sites, the neighbouring structure and the lattice state, which are common for the two patterns (2NN and 3NN). Notice that the keyword neighboring is now followed by two expressions, which define the links between sites 1-2 and 2-3. Note also the use of the & character in the second line following the lattice_state keyword.

The two variants of the pattern are subsequently defined, with the variant followed by a string. When Zacros parses the variant, it will append this string to the name of the cluster followed by an underscore, for instance, the variant 2NN inside the block O_pair will be named as "O_pair_2NN". Parsing of a variant ends when the keyword end_variant is encountered. Inside the variant … end_variant block, one can define the site types, graph multiplicity and cluster energy of the pattern.

The new keyword we come across here is angles, which is followed by an expression with two parts: the first part, before the ":", contains the numbers of three sites separated by two dashes, which define the two rays and the vertex of the angle. The vertex is always the site mentioned second in this expression; here, it is site 2. In our case, ray 1 is the link between sites 2 and 1, and ray 2 is the link between sites 2 and 3. These definitions have to respect the neighbouring structure of the pattern; here, in particular, site 1 has to be a neighbour of site 2 and site 2 a neighbour of site 3. The second part of the expression (after the ":") is the angle in degrees. An angle is positive if ray 2 is located anticlockwise with respect to ray 1. In our case, ray 2 (s₂→s₃) is anticlockwise with respect to ray 1 (s₂→s₁) and therefore the angle is defined as 120° for the 2NN pattern. Clearly, this convention is of no consequence in the case of the 3NN pattern, where the definition of the angle as 180° or -180° makes no difference.

Continuing with the 4NN and 5NN patterns, the Zacros input thereof should be clear now, based on our discussion about the 2NN and 3NN patterns:

cluster O_pair
  sites 4
  neighboring 1-2 2-3 3-4
  lattice_state
    1 O*   1
    & &    &
    & &    &
    2 O*   1

  variant 4NN
    site_types          fcc_t  fcc_t  fcc_t  fcc_t
    graph_multiplicity  2
    angles              1-2-3:120.0  2-3-4:-120.0
    cluster_eng         0.028
  end_variant

  variant 5NN
    site_types          fcc_t  fcc_t  fcc_t  fcc_t
    graph_multiplicity  2
    angles              1-2-3:180.0  2-3-4:180.0
    cluster_eng         0.032
  end_variant

end_cluster

It is important to note that Zacros automatically searchers for mirror images of a pattern in addition to the original one, by changing the sign of all the angles defined. Thus, the definition shown above for the two angles in pattern 4NN, also implies that patterns with the following angles specification will be searched:

    angles              1-2-3:-120.0  2-3-4:120.0

This is a useful feature for proper detection of patterns that are symmetrically equivalent, without having to include additional instructions in the input file. Consider for example the case depicted below:

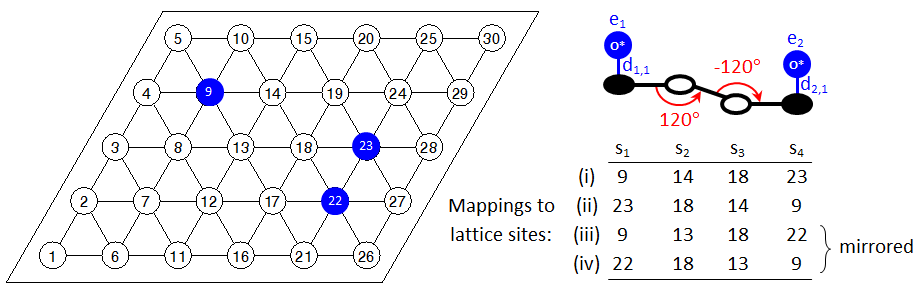
Clearly, the oxygen adatoms occupying sites 22 and 23 are both 4^th nearest neighbours of the oxygen adatom of site 9. Four patterns would be detected as shown in the figure, which are essentially two patterns with graph multiplicity of 2 each. However, if we were to search only for the original pattern (no mirror images), we would have missed the interaction between adatoms on sites 9 and 22. Still though, there may be cases where one may not want to search for mirror images. Therefore, Zacros's default behaviour can be changed by including the keyword no_mirror_images within the variant definition block. This feature will be discussed in more detail in the following section.

One may have noticed that the detection of mirror images for patterns involving sites with unspecified states could result in excessive multiplicities. Consider for instance, the configuration shown below:

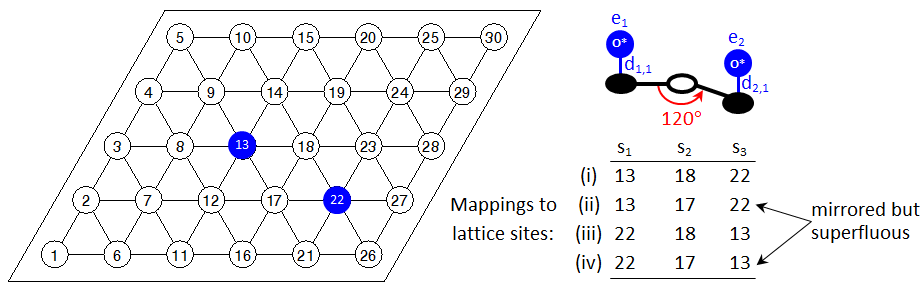
There is only one 2NN pair of oxygen adatoms on the lattice. The possible lattice-to-pattern site mappings are however four; mappings (ii) and (iv) have exactly the same lattice-sites for the pattern-sites 1 and 2 (the ones with the specified states) as mappings (i) and (iii), respectively. The only difference is in the assignment of sites with unspecified states. If Zacros was to detect all of these patterns, the graph multiplicity of the 2NN pattern would be 4. The situation could be even worse for more complicated patterns, resulting in excessive multiplicities and significant computational expense in detecting superfluous patterns. To avoid such issues, Zacros does not iterate over sites with unspecified states while performing pattern detection. Thus, once it has detected mapping (i) it will not try to find additional mappings having the same assignments of the "specified" sites 1 and 3, but different assignment for site 2. Instead, it will proceed with searching for another mapping of sites 1 and 2; it may therefore detect mapping (iii) or mapping (iv), but not both.

The definition of patterns 6NN-8NN is left as an exercise. The full energetics_input.dat, containing the input for these patterns, can be downloaded in the end of this tutorial.