Adsorbate lateral interactions have recently attracted significant focus in the computational catalysis field, as they are responsible for ordering in the adsorbate overlayer, but also influence the activation energies of elementary events. Zacros treats such interactions within the general framework of cluster expansion Hamiltonians. This enables us to include long-range and many-body contributions in a simulation. Brønsted-Evans-Polanyi relations are used to correlate the activation energy of an elementary event with its reaction energy, thereby capturing the influence of neighbouring spectator adsorbates on barriers. This tutorial deals with setting up the Zacros input for a detailed cluster expansion Hamiltonian for O on Pt developed by Schneider and co-workers [J. Catal. (2012) 286: 88-94].
Adsorbate lateral interactions affect both the structure of the overlayer and the energetics of elementary events. They are thus responsible for spatial correlations and adsorbate ordering, and also result in spectator species influencing the stability of initial, transition or final states of elementary events, thereby affecting the activation energies thereof.1 A recent study by Schneider and co-workers2 demonstrated how such effects can be simulated using cluster expansions in Monte Carlo simulation combined with kinetic modelling. Such a cluster expansion Hamiltonian can be set up in Zacros file energetics_input.dat as shown in this tutorial.
Part 1: Energetic interaction patterns
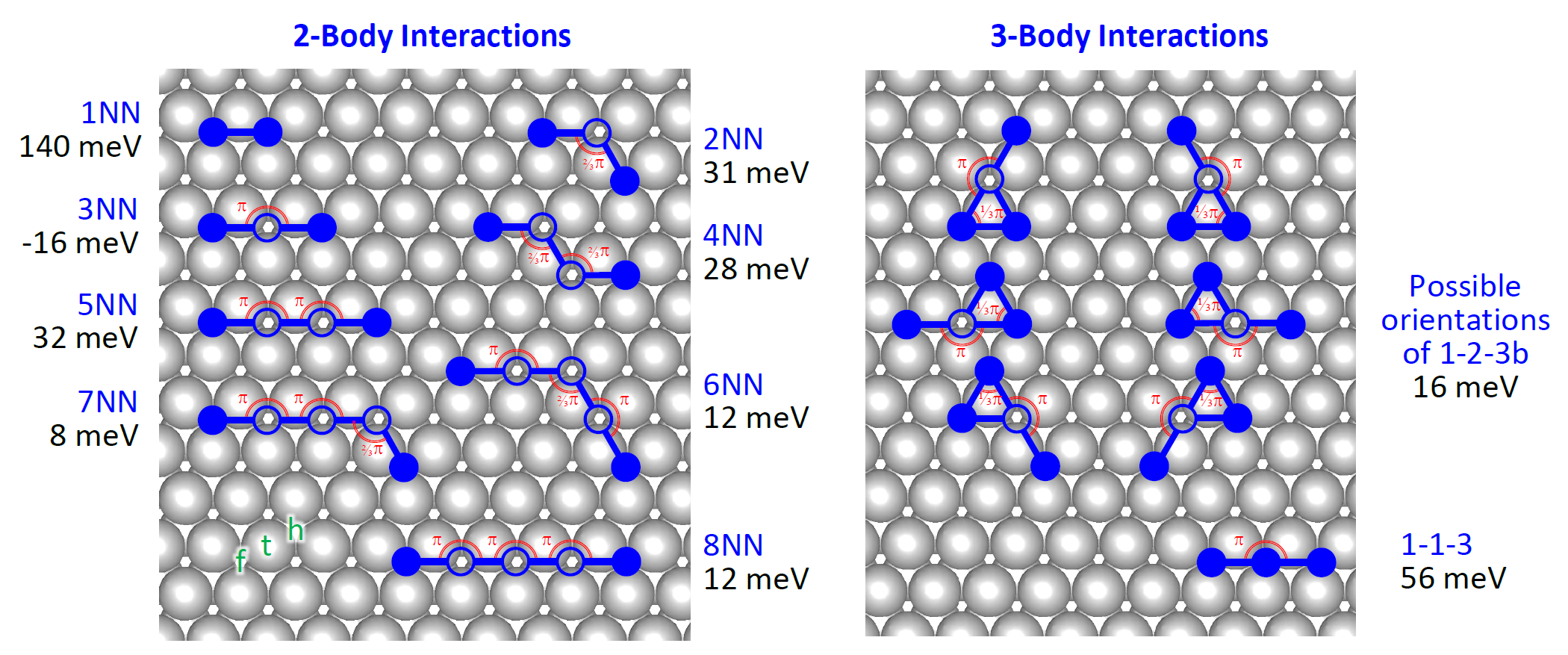
The figure below shows the two- and three-body interaction patterns taken into account by the cluster expansion (CE) in discussion, overlaid on the Pt(111) surface. The different sites of this surface are marked on the bottom left of the first panel: top (t), fcc hollow (f) and hcp hollow (h). Oxygen binds to the fcc hollow sites, exhibiting a formation energy of -1368 meV, with respect to gas O2 at the zero-coverage limit. The two-body patterns (also referred to as "clusters" or "figures") are shown in the left panel below, and include up to 8th nearest-neighbour interactions. Filled circles correspond to sites occupied by oxygen adatoms, whereas open circles correspond to sites that may or may not be occupied, in other words, the state of these sites is unspecified. Moreover, note that we only display one orientation for each pattern; due to the symmetry of the lattice, there are six 1NN, 2NN, 3NN, 5NN, 6NN and 8NN orientations, and also twelve 4NN and 7NN orientations. Zacros's graph-theory-based pattern detection takes care of these possible multiple orientations, without the user having to define new patterns for the different orientations.
The energetic contributions of all patterns, also known as the effective cluster interaction (ECI) parameters, appear in units of meV. Zacros uses the lattice-gas convention for these values, as opposed to the Ising model convention used in the original paper by Schneider and co-workers.2 For the details on the mapping between the two conventions and how to make conversions please refer to the supplementary material of Ref. 3.
The three-body terms are shown on the right of the figure below. There are two such patterns: the 1-2-3b and the 1-1-3. For the 1-2-3b pattern we require that a top site is enclosed by the two neighbouring oxygens and the unspecified site, in accordance with the original paper by Schneider and co-workers.2 Rotating the 1-2-3b pattern by 60 degrees results in a 1-2-3a pattern, in which two neighbouring oxygens and the unspecified site enclose an hcp hollow site. Thus, there are only six acceptable orientations for the 1-2-3b pattern, the ones shown in the figure below.
In addition to the patterns shown below and the oxygen adatom binding energy, the cluster expansion will also include a "background" contribution to the total energy, equal to 12 meV per site (irrespective of its state, vacant or occupied). Such a background term may result from fitting the terms of the expansion to first-principles data the contributes a constant amount of energy for a lattice with fixed size. It is only included for cross-compatibility purposes, as it does not contribute towards energy differences which are of importance to the dynamics of the simulated system.
Part 2: Input for single-body terms
Preliminary schematics in preparation for input
We now proceed to set up the Zacros energetics_input.dat file describing our cluster expansion. To correctly define the patterns in energetics_input.dat, it is often helpful to make a schematic of the binding configuration wherein we clearly number the sites, adsorbate molecules and dentates thereof. This drawing process can be accomplished by following these steps:
- Draw all the sites involved in the pattern.
- If more than one sites are involved, draw all the links between the sites indicating which sites are neighbours.
- Number all the sites in the pattern, as s1, s2,…
- Draw all the adsorbate entities participating on the pattern, clearly indicating the species type for each entity.
- Draw the bonds between adsorbates and sites, to clearly indicate which adsorbate occupies which site (or sites, if there are multidentate adsorbates). At this stage, sites with unspecified states will be numbered but not occupied by any adsorbates. If desired, mark these sites explicitly as unspecified.
- Number all adsorbates (entities) as e1, e2,…
- Number all dentates as d1,1, d1,2, …, d2,1, d2,2,… The first index in this numbering system is the entity number, and the second is the dentate number.
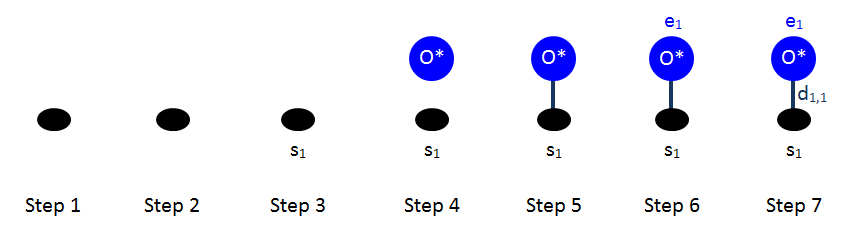
Let us first demonstrate these steps for two very simple patterns: the "AnySite" pattern that contributes the background energy of 12 meV per site irrespective of state (vacant/occupied), and the "O_Point" pattern for a single oxygen adatom on an fcc site.
The figure below shows the steps for drawing the "AnySite" pattern: notice that there is no change from step 1 to step 2, since there is only one site involved (no neighbouring structure). Similarly, there is no change from step 3 to 4, since there a no adsorbates participating in this pattern. The state of the site is unspecified, as indicated by the open marker in step 5. Subsequent steps are not performed, since there are no adsorbates to assign numbers to.

For the case of the oxygen adatom, the drawings are shown below. In this case, we have one adsorbate bound with dentate number 1 (its only dentate) to the single site of the pattern.
Input for the single-body terms
We will now work on the Zacros input that defines these patterns. The file energetics_input.dat always starts with the keyword energetics, followed by one or more blocks of instructions contained within keywords cluster … end_cluster. Each such block describes an energetic pattern. The parsing of the file finished when Zacros encounters the keyword end_energetics.
Thus, for the "AnySite" pattern we write:
cluster AnySite
Then, the number of sites involved (one) is defined as follows:
sites 1
Subsequently, we define the occupancy of the site involved, which is done with the lattice_state keyword. This keyword is followed by as many lines of input as the number of sites in the pattern (in this case only one). Each line contains three words: the first is the number of the entity/adsorbate occupying the corresponding site, the second is the species name occupying that site, and the last word is the dentate number with which the entity binds to that site. In the case of a site with unspecified state, all three words are replaced with the character &:
lattice_state
& & &
Subsequently, we can optionally define the types of sites and the graph multiplicity of the pattern, and we have to specify the pattern's ECI (the energy contribution). The site types are defined by the optional keyword site_types, followed by as many words as the number of sites in the pattern. These words have to correspond to names of site type as defined in file lattice_input.dat. In our case, we assume that we work with a single site type named "fcc_t". We can thus mention explicitly that we require the sites to be of type "fcc_t" for this pattern to be detected:
site_types fcc_t
This specification is however not compulsory: if we don't mention anything about the site types, Zacros will detect the energetic interaction patterns on the lattice based on the neighbouring (connectivity) of the sites and their state. Here we have a single site type anyway, so including or omitting the site_types keyword makes no difference.
The multiplicity is defined by the optional keyword graph_multiplicity, whereas the energy contribution is specified with the keyword cluster_eng. If graph_multiplicity is absent, a default value of 1 is used for the multiplicity. This feature exists for cross-compatibility with other KMC software codes: when Zacros detects this pattern on the lattice, it will add a contribution to the total energy equal to the cluster energy divided by the multiplicity. This is useful, for instance, in the case of a symmetric pairwise pattern, which will be detected twice by the Zacros algorithm. A multiplicity of 2 will correct for this double-counting, as will be discussed in the next section (Part 3). In our case, we have a single-site pattern so the multiplicity can only have a value of 1. Moreover, the ECI value is written in units of eV:
graph_multiplicity 1
cluster_eng 0.012
The cluster specification block ends with the keyword end_cluster.
For the case of the oxygen adatom, we have to specify the state of the site involved in the pattern. We thus observe that site number 1 is occupied by dentate 1 of entity number 1, which is a O* (see figure above). The site type is fcc_t, the graph multiplicity is 1, and the cluster energy is -1.368 eV. Therefore:
cluster O_Point
sites 1
lattice_state
1 O* 1
site_types fcc_t
graph_multiplicity 1
cluster_eng -1.368
end_cluster
Part 3: Input for two-body terms
Nearest-neighbour interactions and the concept of graph multiplicity
Let us now proceed with the two-body terms. Following the rules of the previous section, we can draw the schematic of the 1NN interaction pattern, shown previously in Part 1:
The Zacros input for this cluster is shown below.
cluster O_pair_1NN
sites 2
neighboring 1-2
lattice_state
1 O* 1
2 O* 1
site_types fcc_t fcc_t
graph_multiplicity 2
cluster_eng 0.140
end_cluster
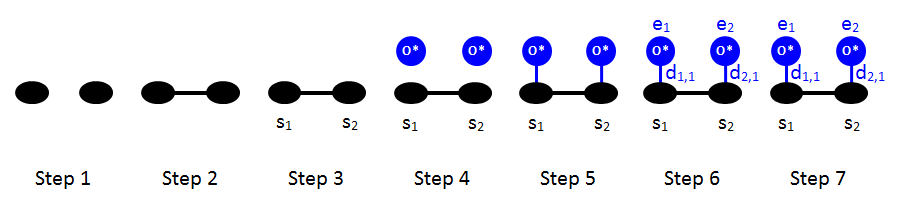
The new keyword neighboring specifies that sites 1 and 2 must be neighbours in the pattern. Moreover, since there are two sites in the pattern, there are now two lines following lattice_state. The first line corresponds to site 1 and the second to site 2. In each line, the first word is the entity number, the second is the species type, and the third is the dentate occupying the corresponding site. In line with the above figure, our input specifies that site 1 is occupied by entity 1, which is an oxygen adatom, and binds therein with dentate 1 (the only dentate for this species). Moreover, site 2 is occupied by entity 2, which is an oxygen adatom, and binds therein with dentate 1.
Some discussion on the graph multiplicity is useful at this point. When Zacros computes the total energy of the system, it has to detect all the occurrences of the known (i.e. defined in the input) energetic interaction patterns on the lattice. To do so, it solves a sequence of subgraph isomorphism problems, trying to match the known pattern with arrangements of adsorbates on the lattice. If a given pattern is symmetric, the subgraph isomorphism problem may give the same solution more than once. Consider for example the following arrangement of a pair of oxygen adatoms on a lattice with 30 sites:
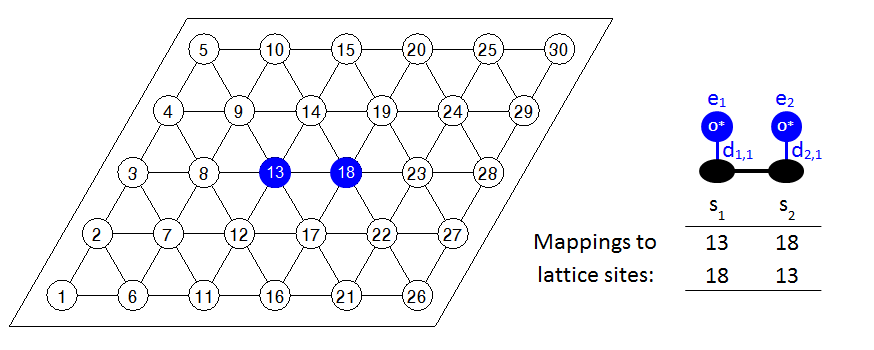
Zacros will detect that this is a 1NN pair of sites and will assign lattice-site 13 as pattern-site 1 and lattice-site 18 as pattern-site 2. However, there is no reason why lattice-site 18 can't be pattern-site 1, and lattice-site 13 pattern-site 2. In fact, this combination will be detected as another valid pattern by Zacros. We therefore see that the same pattern is detected twice, because of the symmetric arrangements of adsorbates therein. Consequently, the graph multiplicity is defined as the number of times a distinct pattern is detected by solving the subgraph isomorphism problem. In our case, the graph multiplicity is 2, so Zacros will add a contribution of 0.070 eV (0.140/2) per pattern to the energy of the system, bringing the total contribution to the correct value of 0.140 eV.
Long-range interactions: variants, angles and sites with unspecified state
We move on to the specification of long-range pairwise additive interactions, which are slightly more complicated. Consider the 2NN and 3NN patterns displayed below:
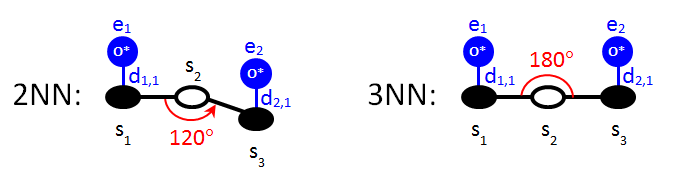
Both patterns involve three sites; the first and the third are occupied by oxygen and the second site has an unspecified state. Site 1 neighbours with site 2, and site 2 neighbours with site 3. The only difference between these two patterns is the angle between the vectors s2→s1 and s2→s3. Of course, the ECIs of the patterns are different as well. To make the input more concise, one can use the keyword variant. The Zacros input for these two patterns can be thus combined into one block that reads as follows:
cluster O_pair
sites 3
neighboring 1-2 2-3
lattice_state
1 O* 1
& & &
2 O* 1
variant 2NN
site_types fcc_t fcc_t fcc_t
graph_multiplicity 2
angles 1-2-3:120.0
cluster_eng 0.032
end_variant
variant 3NN
site_types fcc_t fcc_t fcc_t
graph_multiplicity 2
angles 1-2-3:180.0
cluster_eng -0.016
end_variant
end_cluster
In the first part of this block, we specify the number of sites, the neighbouring structure and the lattice state, which are common for the two patterns (2NN and 3NN). Notice that the keyword neighboring is now followed by two expressions, which define the links between sites 1-2 and 2-3. Note also the use of the & character in the second line following the lattice_state keyword.
The two variants of the pattern are subsequently defined, with the variant followed by a string. When Zacros parses the variant, it will append this string to the name of the cluster followed by an underscore, for instance, the variant 2NN inside the block O_pair will be named as "O_pair_2NN". Parsing of a variant ends when the keyword end_variant is encountered. Inside the variant … end_variant block, one can define the site types, graph multiplicity and cluster energy of the pattern.
The new keyword we come across here is angles, which is followed by an expression with two parts: the first part, before the ":", contains the numbers of three sites separated by two dashes, which define the two rays and the vertex of the angle. The vertex is always the site mentioned second in this expression; here, it is site 2. In our case, ray 1 is the link between sites 2 and 1, and ray 2 is the link between sites 2 and 3. These definitions have to respect the neighbouring structure of the pattern; here, in particular, site 1 has to be a neighbour of site 2 and site 2 a neighbour of site 3. The second part of the expression (after the ":") is the angle in degrees. An angle is positive if ray 2 is located anticlockwise with respect to ray 1. In our case, ray 2 (s2→s3) is anticlockwise with respect to ray 1 (s2→s1) and therefore the angle is defined as 120° for the 2NN pattern. Clearly, this convention is of no consequence in the case of the 3NN pattern, where the definition of the angle as 180° or -180° makes no difference.
Continuing with the 4NN and 5NN patterns, the Zacros input thereof should be clear now, based on our discussion about the 2NN and 3NN patterns:
cluster O_pair
sites 4
neighboring 1-2 2-3 3-4
lattice_state
1 O* 1
& & &
& & &
2 O* 1
variant 4NN
site_types fcc_t fcc_t fcc_t fcc_t
graph_multiplicity 2
angles 1-2-3:120.0 2-3-4:-120.0
cluster_eng 0.028
end_variant
variant 5NN
site_types fcc_t fcc_t fcc_t fcc_t
graph_multiplicity 2
angles 1-2-3:180.0 2-3-4:180.0
cluster_eng 0.032
end_variant
end_cluster
It is important to note that Zacros automatically searchers for mirror images of a pattern in addition to the original one, by changing the sign of all the angles defined. Thus, the definition shown above for the two angles in pattern 4NN, also implies that patterns with the following angles specification will be searched:
angles 1-2-3:-120.0 2-3-4:120.0
This is a useful feature for proper detection of patterns that are symmetrically equivalent, without having to include additional instructions in the input file. Consider for example the case depicted below:
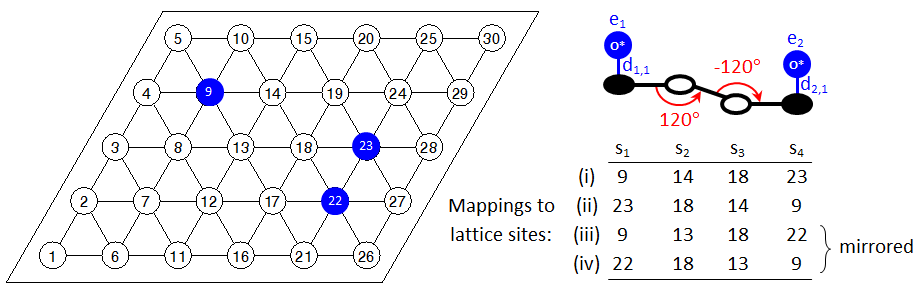
Clearly, the oxygen adatoms occupying sites 22 and 23 are both 4th nearest neighbours of the oxygen adatom of site 9. Four patterns would be detected as shown in the figure, which are essentially two patterns with graph multiplicity of 2 each. However, if we were to search only for the original pattern (no mirror images), we would have missed the interaction between adatoms on sites 9 and 22. Still though, there may be cases where one may not want to search for mirror images. Therefore, Zacros's default behaviour can be changed by including the keyword no_mirror_images within the variant definition block. This feature will be discussed in more detail in the following section.
One may have noticed that the detection of mirror images for patterns involving sites with unspecified states could result in excessive multiplicities. Consider for instance, the configuration shown below:
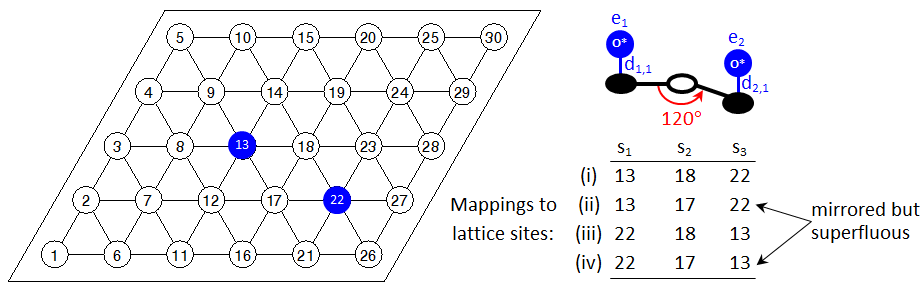
There is only one 2NN pair of oxygen adatoms on the lattice. The possible lattice-to-pattern site mappings are however four; mappings (ii) and (iv) have exactly the same lattice-sites for the pattern-sites 1 and 2 (the ones with the specified states) as mappings (i) and (iii), respectively. The only difference is in the assignment of sites with unspecified states. If Zacros was to detect all of these patterns, the graph multiplicity of the 2NN pattern would be 4. The situation could be even worse for more complicated patterns, resulting in excessive multiplicities and significant computational expense in detecting superfluous patterns. To avoid such issues, Zacros does not iterate over sites with unspecified states while performing pattern detection. Thus, once it has detected mapping (i) it will not try to find additional mappings having the same assignments of the "specified" sites 1 and 3, but different assignment for site 2. Instead, it will proceed with searching for another mapping of sites 1 and 2; it may therefore detect mapping (iii) or mapping (iv), but not both.
The definition of patterns 6NN-8NN is left as an exercise. The full energetics_input.dat, containing the input for these patterns, can be downloaded in the end of this tutorial.
Part 4: Input for three-body terms
The 1-2-3 patterns
The most complicated of the two three-body interaction terms is the 1-2-3b pattern, which is named so because it contains one 1st nearest-neighbour pair of oxygen adatoms, as well as one 2nd and one 3rd nearest-neighbour pair. The "b" in the name of the pattern means that the triangle formed by the nearest-neighbour oxygen adatoms and the unspecified site has to enclose a top site, as discussed previously in Part 1 of this tutorial. In the case that the triangle encloses an hcp hollow site, the pattern is the 1-2-3a. In the figure below, we show all possible orientations of the 1-2-3a and the 1-2-3b patterns, in the left and right panels, respectively. For our simulations we want to exclude the 1-2-3a patterns, and only take into account the 0.016 eV contributions of the 1-2-3b patterns.
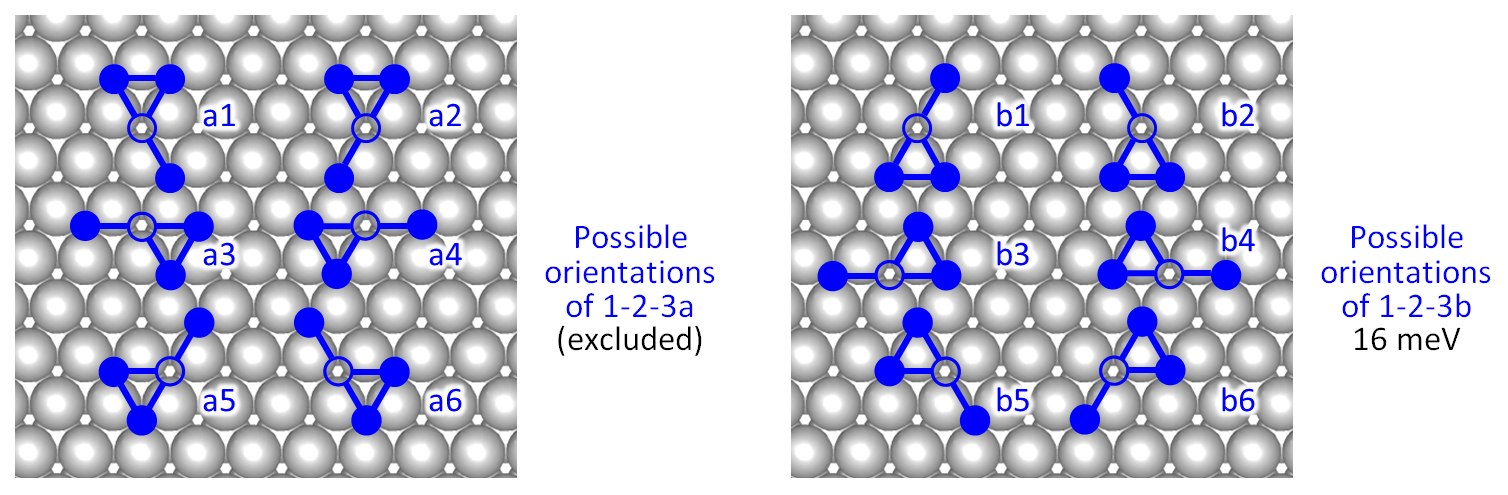
By inspecting the above figure, we realise that taking into account only the "b" patterns necessitates explicit definitions of the six possible orientations. For example, one might be tempted to define patterns b1 and b2, prevent the detection of mirror images with the no_mirror_images keyword, and let Zacros deal with the rotations, thereby detecting also b3-b6. The problem with this approach will be that a 180°rotation of pattern b1 will give pattern a2 which we would like to exclude. Similarly b2 can be rotated to give a1, etc.
Absolute orientations
To avoid such problems Zacros allows the precise definition of the desired rotational orientation with the keyword absl_orientation. This keyword is followed by an expression in two parts, similar to the angles keyword. The first part comes before a ":" and contains the numbers of two sites of the pattern separated by a dash; this defines a vector. The second part gives the angle of this vector with respect to x-axis, in particular with respect to the unit vector (1,0). Thus, this line of input may read:
absl_orientation 1-2:180.0
Therefore, combining the keywords angles, no_mirror_images, and absl_orientation, enables the precise definition of the desired orientation of a pattern, whenever needed. To illustrate this, let us draw a schematic of the b1 orientation of the 1-2-3b pattern:
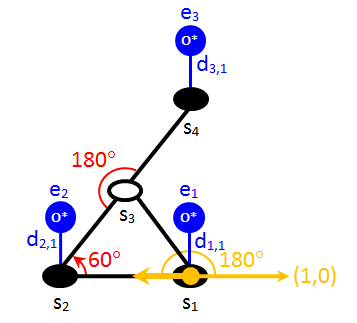
There is quite a lot of information in the above schematic, and we have already discussed how the neighbouring pattern and the site occupancies are translated to Zacros input. Thus, one can verify that the first few lines of the input should be:
cluster O_triplet_1-2-3b
sites 4
neighboring 1-2 1-3 2-3 3-4
lattice_state
1 O* 1
2 O* 1
& & &
3 O* 1
We now proceed to define the b1 orientation as a variant:
variant b1
site_types fcc_t fcc_t fcc_t fcc_t
graph_multiplicity 1
angles 1-2-3:60.0 2-3-4:180.0
no_mirror_images
absl_orientation 1-2:180.0
cluster_eng 0.016
end_variant
In the above instructions, the site types are specified as fcc, as before, and the graph multiplicity is 1 because there is no re-mapping of the sites that would result in a new indistinguishable pattern (i.e. there is no multiplicity of orientations). We define two angles: the one of 180° clearly has to be specified, for the correct positioning of site 4. The need for the specification of the 60° angle is a bit more subtle: one might argue that, since sites 1, 2 and 3 form a triangle (see neighbouring structure), one could omit the angle between links s2→s1 and s2→s3. However, if this angle specification is omitted, the keyword no_mirror_images becomes ineffective, as it would only prevent Zacros from detecting a pattern with an angle of -180° between sites 2, 3 and 4 (which of course has no effect). Thus, there is nothing stopping the detection, for instance, of the a1 orientation shown in the first picture of this section. Hence, the correct input has to include the 60° angle specification.
The keyword absl_orientation, defines the angle between the vector s1→s2 and the x axis, as shown in the previous picture (orange vectors and angle). As already discussed, this keyword in combination angles and no_mirror_images enables the precise specification of the desired orientation. Finally, the cluster energy is set to 0.016 eV. The remaining orientations (b2-b6) are left as an exercise and are included in the energetics_input.dat file in the end of this tutorial.
The 1-1-3 pattern
The last pattern of this cluster expansion Hamiltonian is the triplet 1-1-3, which contains three oxygen adatoms, arranged in such a way that there are two first-nearest-neighbour pairs and one third nearest neighbour pair. The schematic used to create the Zacros input, along with the input, is shown below. The definition of this pattern makes use of concepts we have already discussed and is rather straightforward. It would still be instructive to convince oneself that the graph multiplicity of this pattern is 2.
cluster O_triplet_1-1-3
sites 3
neighboring 1-2 2-3
lattice_state
1 O* 1
2 O* 1
3 O* 1
site_types fcc_t fcc_t fcc_t
graph_multiplicity 2
angles 1-2-3:180.0
cluster_eng 0.056
end_variant
end_cluster
This concludes the tutorial. The full input file is provided via the link below:
Download energetics_input.dat.
References
- M. Stamatakis (2015). "Kinetic modelling of heterogeneous catalytic systems". Journal of Physics: Condensed Matter 27: 013001 (doi: 10.1088/0953-8984/27/1/013001)
- C. Wu, D. J. Schmidt, C. Wolverton, W. F. Schneider (2012). "Accurate coverage-dependence incorporated into first-principles kinetic models: catalytic NO oxidation on Pt(111)", Journal of Catalysis 286: 88-94 (doi: 10.1016/j.jcat.2011.10.020)
- W. Nielsen, M. d’Avezac, J. Hetherington, M. Stamatakis (2013). “Parallel kinetic Monte Carlo simulation framework incorporating accurate models of adsorbate lateral interactions”. Journal of Chemical Physics 139(22): 224706 (doi: 10.1063/1.4840395)