Part 1: Preliminary considerations
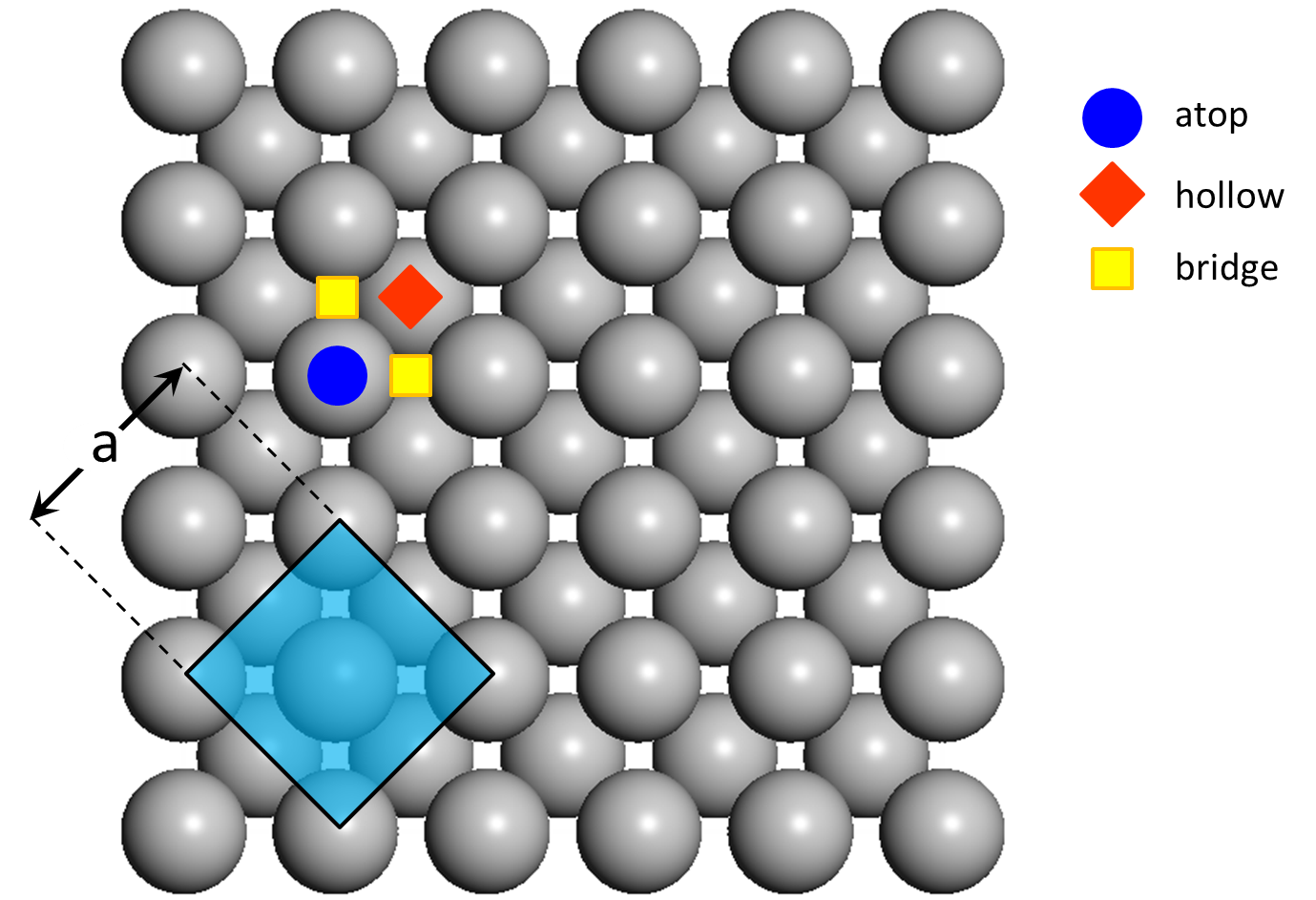
In the (100) surface of an FCC metal, each atom is surrounded by four neighbouring atoms and one can discern three site types: atop, 2-fold bridge and 4-fold hollow. The surface is shown schematically below, highlighting also the unit cell of the FCC crystal and the lattice constant, which for the case of Pd for example is a = 3.8907 Å.
In order to create a lattice that will be appropriate for our simulations and will not contain unecessary detail that may hamper the simulation, we need to answer the following questions:
- Which sites are important?
Density functional theory calculations can reveal the sites which the molecules of interest bind to most strongly. If the most stable configurations of our reactant and intermediate species bind to say the atop and hollow sites, and binding to the bridge site is much weaker, we only need to consider the former two sites, i.e. we can neglect the bridge site as irrelevant.
Of course, when comparing binding energies on different sites to determine the most stable configurations, we have to keep in mind that depending on the temperature of the simulation, we may or may not be able to safely neglect some configurations. In particular, a difference of 0.05 eV between the binding energies of a species on two site types may be significant at low temperatures, and therefore considering only the most site may be enough. At high temperatures, however, the lower binding energy site may be highly populated as well, which would necessitate taking into account both sites in the lattice definition.
- How to connect the sites?
Site connectivity in the lattice is determined by the elementary reaction events we need to model, as well as the energetic interactions between adsorbed species. If you are unfamiliar with these concepts, please refer to the tutorials Ziff-Gulari-Barshad Model in Zacros and Cluster Expansion for Oxygen on Pt(111). The rule is that if two sites participate in an elementary reaction or an energetic interaction pattern, then they have to be connected, either directly, or indirectly via one or more other sites. This enables the Graph-Theoretical KMC algorithm to detect the patterns efficiently by solving subgraph isomorphism problem. For instance, if a diffusional hop can happen from a hollow site to another, these sites must be connected in our lattice.
Let us assume that for our purposes it is enough to model the atop and 4-fold hollow sites only. Also, let us decide to model all three possible links between these two site types: atop-atop, hollow-hollow and atop-hollow. In the following section we will discuss how to draw a lattice picture that can be translated to Zacros input in a straightforward way.