If you are wondering "What can Kinetic Monte Carlo (KMC) do for me?" this article is for you. It is intended as a discussion more than a tutorial in the strict sense, but with a (hopefully) clear learning aspect. Thus, we will highlight the benefits of KMC compared to simpler approaches, such as mean-field (micro-kinetic or phenomenological) models, taking as an example a prototypical system: the CO oxidation reaction. Of course, the main ideas behind this discussion hold true for more complicated reactions as well.
So the net reaction we will discuss is:
CO + ½O2 → CO2
When this happens on the surface of a catalyst (e.g. the (111) facet of a Pd nano-crystal) the reaction could proceed via the following three elementary steps:
CO + * ↔ CO* (reversible adsorption of CO on an empty catalytic site)
O2 + 2* ↔ 2O* (reversible dissociative adsorption of O2 on two neighbouring empty catalytic sites)
CO* + O* → CO2 + 2* (reversible adsorption of CO on an empty catalytic site)
In the notation we just used and will adopt throughout, * denotes an empty site, whereas A* an adsorbate (bound species A).
Traditional kinetic models
Langmuir-Hinshelwood-type models can describe the kinetics of this reaction mechanism by invoking a number of assumptions:
- Each site can be occupied by at most one adsorbate. This is sometimes referred to as the "exclusion principle". It is usually true, although there are some notable exceptions e.g. two CO molecules can bind to a cobalt site. One can circumvent this problem by defining a new species e.g. C2O2*.
- All catalytic sites are equivalent. This means that CO*, for instance, has the same "stability" (quantified by the binding energy) at any site on the surface. Consequently the probability of finding any site occupied by CO* is equal to the coverage of CO*. This assumption is not true in general: catalytic nanoparticles expose a variety of sites with different coordination numbers, onto which adsorbates bind with different strengths. Still though, one can formulate a more complicated Langmuir-Hinshelwood model taking into account the various binding states for the same species.
- Adsorption/desorption steps are quasi-equilibrated. This assumption is typically employed in Langmuir-Hinshelwood models and makes things easy by providing analytical expressions of the coverage of each surface reactant with respect to the gas phase composition, pressure and temperature. Of course one can easily formulate more complicated models in which the coverages are variables of a differential equation system to be solved for.
- No spatial correlations are observed between adsorbates. To visualize this, imagine a pair of sites A and B and let us only consider CO adsorption. The assumption can be restated as: the probability of finding a CO* on site B, does not depend on the occupancy of site A. Thus, the probability of finding a pair of CO* adsorbates next to each other is θCO·θCO = θCO2. This is a rather limiting assumption: imagine what would happen is CO adsorbates exerted repulsive interactions between each other. Then the real probability of finding a pair of COs could be much lower than θCO2. Likewise, imagine what would happen (in the case of pure O2 adsorption) if O* diffusion was not very fast: since O2 adsorbs dissociatively, one would find pairs of sites occupied by O* more frequently than θO2.
- Kinetic constants are independent of coverage. Thus, a CO oxidation elementary event (CO* + O* → CO2) is assumed to have the same kinetic rate constant, koxi, irrespective of whether the two reactants are in low versus high coverages. The reaction rate will be given by koxi·θCO·θO, where the product of the two coverages is essentially the probability of finding a reactive CO*-O* pair and koxi is indeed constant. However, it is known that rate "constants" are coverage-dependent: the activation energy of the CO oxidation elementary event drops at high coverages, and the reaction tends to proceed faster. This makes sense intuitively: when the catalytic surface is cramped with molecules, the repulsions between the reacting CO* and O* and the (several) CO* and/or O* spectators destabilize the reactant configuration, thereby lowering the reaction barrier.
We therefore see already that some of the assumptions just noted pose limitations on the validity of the Langmuir-Hinshelwood model. Under these assumptions, the CO oxidation rate expression is:
RateLH = koxi·θCO·θO
where
θCO = KCO·PCO/(1+KCO·PCO+√(KO2·PO))
θO = √(KO2·PO)/(1+KCO·PCO+√(KO2·PO))
KCO = kads,CO/kdes,CO
KO2 = kads,O2/kdes,O2
A simple KMC simulation
There is a lot of theory and mathematical formalism behind the kinetic Monte Carlo (KMC) algorithm and how/why it works, but for all practical purposes it can be thought of as a computer game that uses random numbers. The game is being played on a lattice, each site of which can be occupied by either of the two adsorbates of our example, CO* or O*. The KMC algorithm performs random "moves" (referred to as elementary events) e.g. adding a CO* adsorbate via adsorption at a certain lattice site at some time t1, performing a diffusional hop at some time t2, adding a pair of O* adsorbates via dissociative adsorption at neighbouring sites at t3, performing a diffusional hops of a O* at a time t4 etc. When O* and CO* "meet each other", they also have a certain probability of reacting towards CO2 gas, so KMC also simulates such events once in a while. Important points to note are that a typical KMC algorithm:
- executes/realizes elementary events one after the other (one event at time)
- uses random numbers to decide when the next event will take place (t1, t2, ...) and what kind of event it will be (adsorption, desorption, diffusion, reaction etc.)
- generates these random numbers in such a way that events with higher kinetic constants are executed more frequently, as expected (i.e. these random numbers are not "completely random").
In fact, there are theorems from mathematical physics assuring us that if we simulate a KMC model for CO oxidation which is a faithful representation of Langmuir-Hinshelwood kinetics, we should get the exact same predictions as the equations listed in the previous section. This is shown in the simulations below:
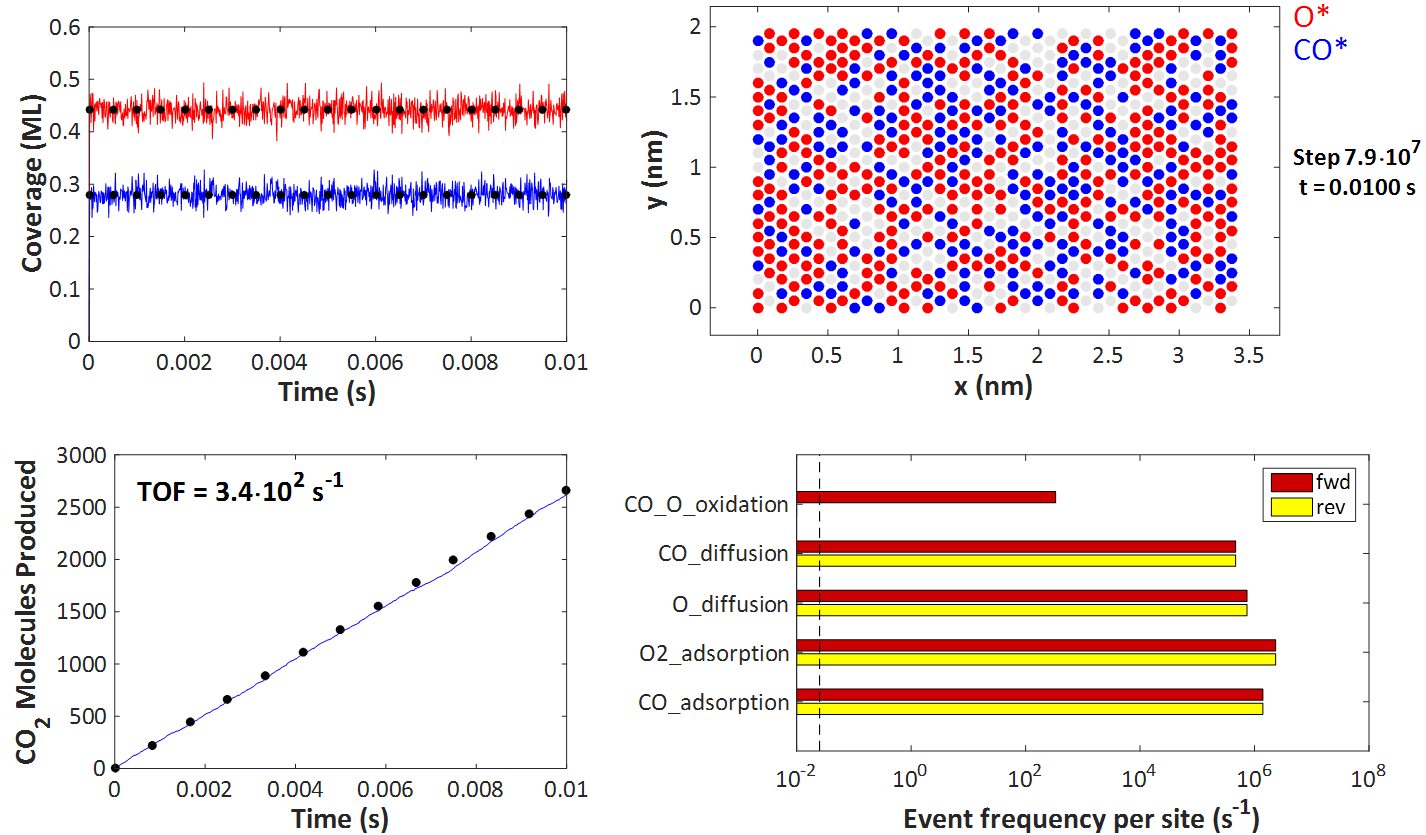
The top left plot depicts the coverages of O* and CO* over time, which quickly reach steady state (the transients are too short to be apparent). The black dots represent the predictions of the Langmuir-Hinshelwood model, and it is evident that KMC agrees with this model. Of course, there is some noise because of the random (stochastic) nature of KMC, but the aforementioned theorems inform us that simulating larger and larger lattices will bring the noise down, making the KMC predictions indistinguishable from those of the Langmuir-Hinshelwood deterministic equations.
On the top right plot, one can see a snapshot of the KMC lattice at the end of the simulation. The filled red circles correspond to O*-occupied sites, the blue ones to CO*-occupied sites, whereas the grey circles denote vacant sites. As per assumptions 1 and 2 of the Langmuir-Hinshelwood model, discussed earlier, each site can only be occupied by at most one adsorbate molecule, and all sites are equivalent. We also have no lateral interactions in the KMC model, so there is no discernible ordering on the adlayer.
The bottom right figure compares the KMC prediction for the number of CO2 molecules produced over time (blue line) with that of the Langmuir-Hinshelwood model. In particular, the black dots are on a line with zero intercept and slope equal to RateLH from the equations above. Again, the KMC prediction closely matches that of the Langmuir-Hinshelwood model.
Finally, the bottom right plot portrays a histogram of the reaction statistics. Worth noting is that the event frequency of the CO_O_oxidation event is the turnover frequency (TOF) of 340 s-1, in agreement with the plot on the left just discussed. Moreover, adsorption/desorption and diffusion events are quasi-equilibrated and occur on a much faster timescale than the oxidation event. These observations are in line with assumptions 3 and 4 of the Langmuir-Hinshelwood model (note also that the KMC kinetic constants are indeed constants, i.e. independent of coverage in this simple example).
If you wish to run these calculations in Zacros and check your results, you can obtain the full input and output files via the link below:
Download LangmuirHinshelwood.zip.
A technical point to note when reproducing these results: the value of koxi in the Langmuir-Hinshelwood model must be 6 times the value of the rate constant for the CO_O_oxidation event fed as input to the KMC. The reason is that in our lattice, each site has 6 neighbours (coordination number 6), so the oxidation event is "replicated" across each neighbouring site. Ref. 1 contains more information on the mathematics of this.
Beyond simple: the real power of KMC
The previous section demonstrates what kind of output can KMC generate, and shows that for very simple systems, which can be modelled analytically, the KMC predictions are in perfect agreement with the analytical results (e.g. from Langmuir-Hinshelwood modelling). So what is the motivation for using KMC in the first place? The answer is simple: catalytic systems are complex! Much more complex than what the Langmuir-Hinshelwood model suggests. Even well-studied (and deceptively simple) reactions, like the CO oxidation, exhibit rich and often puzzling behaviour as recent experimental research has demonstrated. KMC modelling has helped unravel such behaviour and explain the experimental observations. In the following, we summarize modelling contributions from our team on the CO oxidation reaction on two classes of materials (Pd surface, Au nanoclusters), highlighting the advantages of KMC against simple models. The discussion is kept at a high-level, intended to "whet the appetite" of the newly initiated reader, who can consult the cited papers for more technical details.
CO oxidation on Pt(111): a deceptively simple system
A major assumption in Langmuir-Hinshelwood type of models is that the adlayer is ideal and well-mixed. However, the presence of adsorbate-adsorbate lateral interactions leads to spatial correlations and coverage-dependent activation energies. KMC simulation was recently employed to show that such effects can shape the observed kinetics, most notably, the reaction order.2,3 The study was motivated by an experiment carried out by Nakai, Kondoh and co-workers, who dosed the Pt(111) surface with oxygen, exposed the system to a CO atmosphere and measured several kinetic parameters (orders with respect to CO(g) and O*, apparent activation energies) while also observing the structure of the adlayer through XPS.4 What was particularly interesting, was the different reaction orders with respect to O* at high and low temperatures (320 K, 190 K). At the high temperature, the experiment showed half-order kinetics which were attributed to the formation of O* islands that react with CO* only at their periphery. The length of the periphery scales with the square root of their area, and the total area is proportional to the O* coverage; therefore, this simple geometric argument should be enough to explain the observed half-order kinetics with respect to O* coverage at 320 K. However, observations at 190 K showed first-order reaction kinetics with respect to O*, which indicated a well-mixed adlayer. This is where things become counter-intuitive: why would one expect to see islands at 320 K, but not at 190 K? If anything, one would expect the islands to be even more stable at the low temperature, in which case, one would measure half-order kinetics at 190 K as well.
The problem with these arguments is that they completely neglect the effect of lateral interactions on the activation barriers and reaction rates. Detailed first-principles-based5 KMC modelling suggests that in both the high and low temperatures, the adlayer remains relatively well-mixed: as the CO molecules impinge at random positions on the surface, any oxygen clusters quickly dissipate. This "almost well-mixed" behaviour has a positive contribution to the reaction order of 0.9 at 320 K and 0.8 at 190 K (recall that an order of 1.0 means "totally well-mixed" adlayer, and 0.5 means "completely segregated"). However, the effect of lateral interactions on the activation energies is decisive. At the high temperature, the system exhibits mean-field type behaviour; since CO-CO interactions are slightly more strongly repulsive than the other adsorbate-adsorbate interactions, the reactive CO becomes more and more destabilized as the reaction proceeds, making the reaction "go faster" as oxygen gets depleted from the surface (top left panel of figure below). This manifests as a negative contribution to the overall reaction order of about -0.4, bringing the total order to 0.5, half order kinetics! On the other hand, at the low temperature, one has to look into the entire distribution of activation energies as time goes by (bottom right panel of figure below). Proper averaging of the elementary event rates in the presence of these lateral interactions shows that the effect of oxygen coverage is positive (the reaction slows down as oxygen gets depleted; top right panel of figure below), with a total reaction order of about unity.
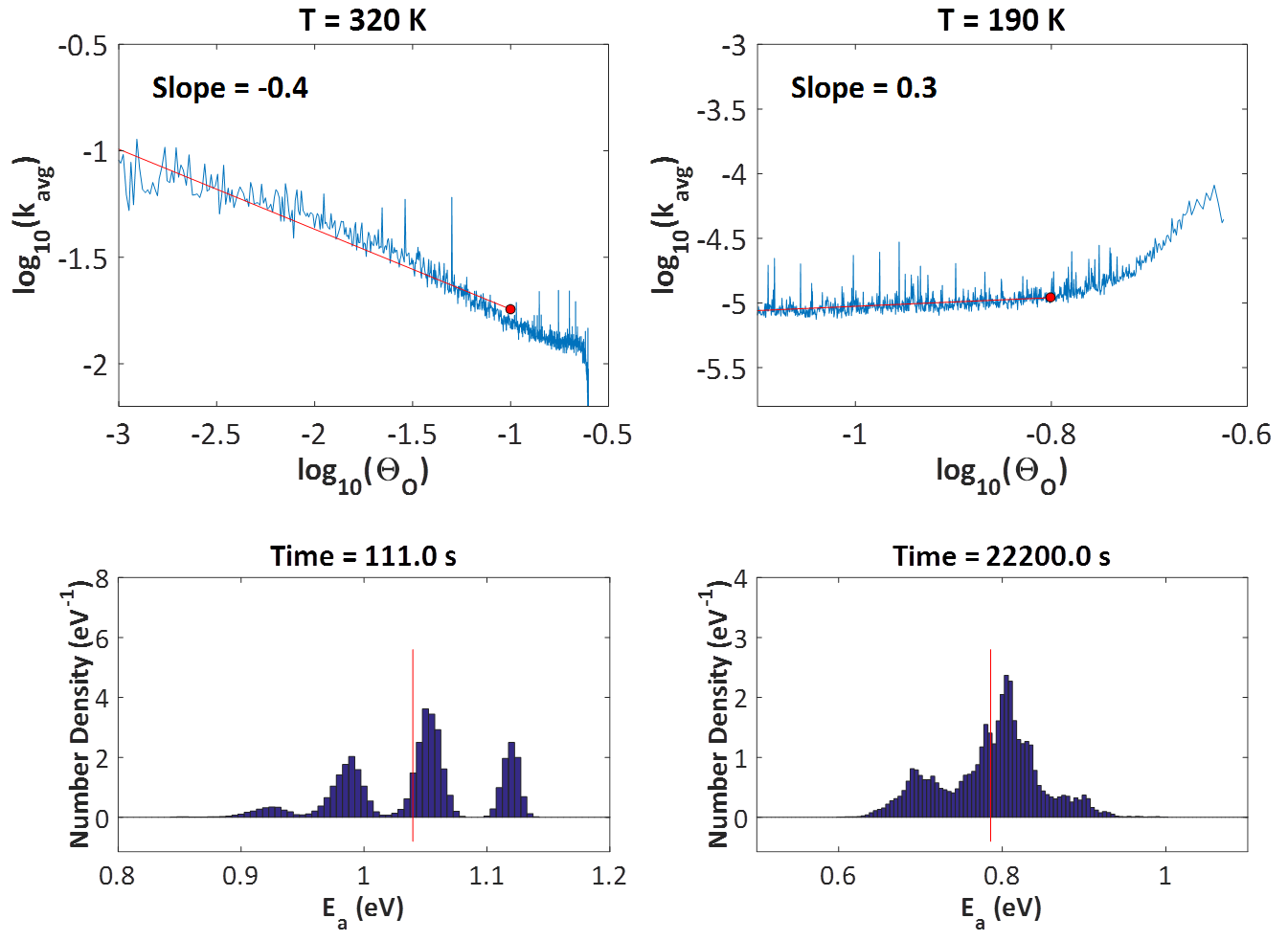
Looking at the histograms of the bottom two panels above, it is worth noting that in the presence of these coverage effects, the activation energy follows a distribution, rather than being equal to a single value. The average is shown by the red vertical lines, and it is evident that there are events with much higher activation energies, but also events with much lower activation energies. The latter contribute much more to the observed overall rate.
CO oxidation on Au nanoclusters
In the previous system, the catalyst was an extended flat surface and complications arose from the presence of lateral interactions. Things become even more complicated when we look at nanoscale or subnanoscale catalysts. Au (gold) nanoclusters are an excellent example to consider: such clusters expose a variety of sites which have different coordination numbers and therefore different chemical behaviours. The underlying pathways of the CO oxidation chemistry can be rather intricate, involving changes in the morphology of the material (catalyst reconstruction), species that bind to more than one site, competitive routes towards the same product (CO2) but also undesired poisons (such as carbonate, CO3). In addition, talking about coverage in subnanoscale Au clusters becomes tricky: because of the small number of sites, coverage is no longer a continuous variable; it may actually exhibit a "rather discrete" behaviour, e.g. on Au6 the coverage of CO (which binds to top sites; see lattices below) can take only 7 values, 0, 1/6, 2/6,...,1. Therefore, constructing a simple kinetic model formulated as an ordinary differential equation (ODE) becomes problematic: while one could consider the average coverage on an ensemble of such Au6 clusters, but still they would have to start from a detailed discrete model and try some sort of averaging procedure to get to the ODE model.
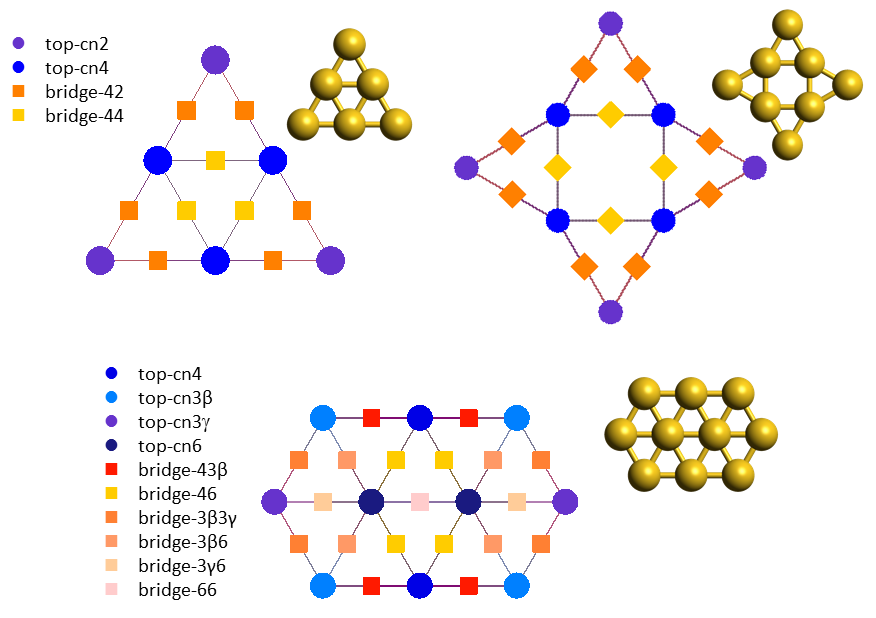
Kinetic Monte Carlo is essentially this "detailed discrete model". Using first-principles KMC models of three Au structures, Au6, Au8 and Au10 (the molecular structures and KMC lattices of which are depicted above), it was possible to perform an in-depth investigation of the kinetics leading to the puzzling reactivity trends observed in experiments. In particular, even though all these clusters expose undercoordinated sites, Au6 appears as inactive, whereas Au8 and Au10 show high activities, with Au8 more catalytically active than Au10 towards CO oxidation.6,7 DFT calculations and KMC simulations exposing the Au clusters to a reactants mixture that contains only CO and O2, showed that Au6 gets poisoned by carbonate early on, whereas Au8 and Au10 do not. On Au8 two parallel oxidation pathways were found to contribute to the activity, with one of the pathways involving catalyst reconstruction. On Au10, a sequence of two elementary steps were found to be rate limiting and lead to the lower activity of this structure compared to Au8. These two steps were: the tilting of O2 from the more stable bidentate to a less stable monodentate configuration, and the subsequent reaction thereof with CO towards CO2.
Conclusion
While simple kinetic models have been instrumental in advancing our understanding of catalytic processes, they have severe limitations. The discussion in this article hopefully highlighted some of these limitations and underscored the importance of KMC simulation tools in overcoming them. The case studies on CO oxidation highlighted showed that KMC can indeed integrate several sources of complexity into a predictive methodological framework that can provide valuable insight into realistic catalyst structures. More complicated chemistries have also been studied with KMC; the interested reader is referred to the review articles of Refs 8 and 9. As the computational tools mature and become more widely adopted, we will be able to delve deeper into the inner workings of catalytic systems, unravelling complexity and developing a fundamental understanding towards the engineering of superior catalysts.
References
- Stamatakis, M. and D. G. Vlachos (2011). "Equivalence of on-Lattice Stochastic Chemical Kinetics with the Well-Mixed Chemical Master Equation in the Limit of Fast Diffusion". Computers and Chemical Engineering, 35(12): 2602-2610. (doi: 10.1016/j.compchemeng.2011.05.008)
- Stamatakis, M. and S. Piccinin (2016). "Rationalising the relation between adlayer structure and observed kinetics in catalysis". ACS Catalysis, 6: 2105-2111. (doi: 10.1021/acscatal.5b02876)
- Piccinin, S. and M. Stamatakis (2014). "CO Oxidation on Pd(111): A First-Principles Based Kinetic Monte Carlo Study". ACS Catalysis, 4: 2143-2152. (doi: 10.1021/cs500377j)
- Nakai, I., H. Kondoh, T. Shimada, A. Resta, J. N. Andersen and T. Ohta (2006). "Mechanism of CO oxidation reaction on O-covered Pd(111) surfaces studied with fast x-ray photoelectron spectroscopy: Change of reaction path accompanying phase transition of O domains." Journal of Chemical Physics 124(22): 224712 (doi: 10.1063/1.2205856)
- First-principles in this context means that the kinetic parameters of the KMC model were obtained from quantum chemistry calculations, in particular, density functional theory.
- Stamatakis, M., Christiansen, M., D. G. Vlachos and G. Mpourmpakis (2012). "Multiscale Modelling Reveals Poisoning Mechanisms on MgO-supported Au Catalysts in CO Oxidation". Nano Letters, 2(7): 3621-3626. (doi: 10.1021/nl301318b)
- Nikbin, N., Austin, N., Vlachos, D., Stamatakis, M. and G. Mpourmpakis (2015). "Catalysis at the Sub-Nanoscale: Complex CO Oxidation Chemistry on a Few Au Atoms". Catalysis Science & Technology, 5(1): 134-141. (doi: 10.1039/C4CY01295J)
- Stamatakis, M. and D. G. Vlachos (2012). "Unravelling the Complexity of Catalytic Reactions via Kinetic Monte Carlo Simulation: Current Status and Frontiers". ACS Catalysis, 2(12): 2648-2663. (doi: 10.1021/cs3005709)
- M. Stamatakis (2015). "Kinetic modelling of heterogeneous catalytic systems". Journal of Physics: Condensed Matter, 27: 013001. (doi: 10.1088/0953-8984/27/1/013001)