Part 4: Input for three-body terms
The 1-2-3 patterns
The most complicated of the two three-body interaction terms is the 1-2-3b pattern, which is named so because it contains one 1st nearest-neighbour pair of oxygen adatoms, as well as one 2nd and one 3rd nearest-neighbour pair. The "b" in the name of the pattern means that the triangle formed by the nearest-neighbour oxygen adatoms and the unspecified site has to enclose a top site, as discussed previously in Part 1 of this tutorial. In the case that the triangle encloses an hcp hollow site, the pattern is the 1-2-3a. In the figure below, we show all possible orientations of the 1-2-3a and the 1-2-3b patterns, in the left and right panels, respectively. For our simulations we want to exclude the 1-2-3a patterns, and only take into account the 0.016 eV contributions of the 1-2-3b patterns.
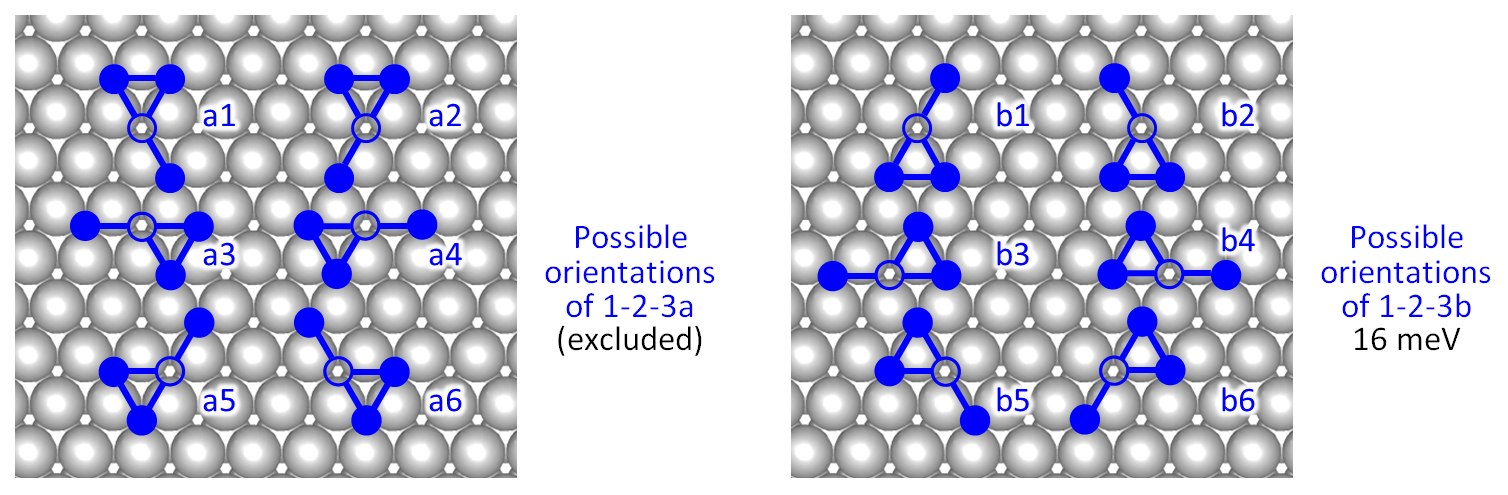
By inspecting the above figure, we realise that taking into account only the "b" patterns necessitates explicit definitions of the six possible orientations. For example, one might be tempted to define patterns b1 and b2, prevent the detection of mirror images with the no_mirror_images keyword, and let Zacros deal with the rotations, thereby detecting also b3-b6. The problem with this approach will be that a 180°rotation of pattern b1 will give pattern a2 which we would like to exclude. Similarly b2 can be rotated to give a1, etc.
Absolute orientations
To avoid such problems Zacros allows the precise definition of the desired rotational orientation with the keyword absl_orientation. This keyword is followed by an expression in two parts, similar to the angles keyword. The first part comes before a ":" and contains the numbers of two sites of the pattern separated by a dash; this defines a vector. The second part gives the angle of this vector with respect to x-axis, in particular with respect to the unit vector (1,0). Thus, this line of input may read:
absl_orientation 1-2:180.0
Therefore, combining the keywords angles, no_mirror_images, and absl_orientation, enables the precise definition of the desired orientation of a pattern, whenever needed. To illustrate this, let us draw a schematic of the b1 orientation of the 1-2-3b pattern:
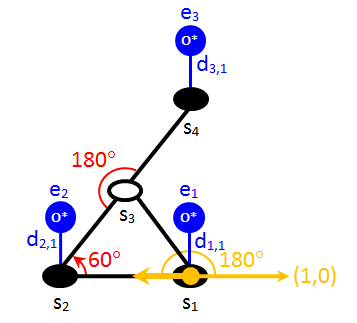
There is quite a lot of information in the above schematic, and we have already discussed how the neighbouring pattern and the site occupancies are translated to Zacros input. Thus, one can verify that the first few lines of the input should be:
cluster O_triplet_1-2-3b
sites 4
neighboring 1-2 1-3 2-3 3-4
lattice_state
1 O* 1
2 O* 1
& & &
3 O* 1
We now proceed to define the b1 orientation as a variant:
variant b1
site_types fcc_t fcc_t fcc_t fcc_t
graph_multiplicity 1
angles 1-2-3:60.0 2-3-4:180.0
no_mirror_images
absl_orientation 1-2:180.0
cluster_eng 0.016
end_variant
In the above instructions, the site types are specified as fcc, as before, and the graph multiplicity is 1 because there is no re-mapping of the sites that would result in a new indistinguishable pattern (i.e. there is no multiplicity of orientations). We define two angles: the one of 180° clearly has to be specified, for the correct positioning of site 4. The need for the specification of the 60° angle is a bit more subtle: one might argue that, since sites 1, 2 and 3 form a triangle (see neighbouring structure), one could omit the angle between links s2→s1 and s2→s3. However, if this angle specification is omitted, the keyword no_mirror_images becomes ineffective, as it would only prevent Zacros from detecting a pattern with an angle of -180° between sites 2, 3 and 4 (which of course has no effect). Thus, there is nothing stopping the detection, for instance, of the a1 orientation shown in the first picture of this section. Hence, the correct input has to include the 60° angle specification.
The keyword absl_orientation, defines the angle between the vector s1→s2 and the x axis, as shown in the previous picture (orange vectors and angle). As already discussed, this keyword in combination angles and no_mirror_images enables the precise specification of the desired orientation. Finally, the cluster energy is set to 0.016 eV. The remaining orientations (b2-b6) are left as an exercise and are included in the energetics_input.dat file in the end of this tutorial.
The 1-1-3 pattern
The last pattern of this cluster expansion Hamiltonian is the triplet 1-1-3, which contains three oxygen adatoms, arranged in such a way that there are two first-nearest-neighbour pairs and one third nearest neighbour pair. The schematic used to create the Zacros input, along with the input, is shown below. The definition of this pattern makes use of concepts we have already discussed and is rather straightforward. It would still be instructive to convince oneself that the graph multiplicity of this pattern is 2.
cluster O_triplet_1-1-3
sites 3
neighboring 1-2 2-3
lattice_state
1 O* 1
2 O* 1
3 O* 1
site_types fcc_t fcc_t fcc_t
graph_multiplicity 2
angles 1-2-3:180.0
cluster_eng 0.056
end_variant
end_cluster
This concludes the tutorial. The full input file is provided via the link below: